正则语言与有穷自动机

本课程为理论计算机科学基础，比起计算机，更像是一门数学课。主要讨论什么是计算。

假定我们定义了计算，那么计算问题可以分成两类。一类是能算的，一类是不能算的。我们会学到一些判断方法。

对于能算的问题，也可以分成容易算的和难计算问题。比如RSA密码学就是利用了一个幂次模方程双向求解的难易度不同设计的。容易计算的问题，对其的计算称为有效计算。如何区别这两类问题，也是本课程的一部分。

0 绪论

本课程主要分为三个部分：

1. 形式语言与自动机
2. 可计算性理论
3. 计算复杂性理论

0.1 历史

1900年，希尔伯特问题10：整系数多项式方程的整数解。穷举算法能否停下来。

1930s, 哥德尔：不完备性定理。

1930s，丘奇的$\lambda$演算，借此定义计算；同时，哥德尔给出(原始)递归函数论，觉得$\lambda$演算不太行。后来发现需要对递归函数做扩充，证明与$\lambda$演算等价。

1930s，图灵带着图灵机来了，图灵机又证明和以上的两种计算方法等价，而且在简洁性方面胜出太多。最后用图灵机作为计算的标准，史称丘奇图灵论题。

1956年，DFA的概念诞生；59年，NDFA的概念诞生，向计算中引入了非确定性。

1965年，P vs NP问题提出

1970年，NP完全得到证明。

以上所有历史均出自于课堂，如若时间对不上，纯属意外。此处毫无历史虚无主义的倾向和想法。

0.2 预备知识

预备知识主要是字符串和语言的描述

定义字母表为任意一个非空有穷集合，元素称为该字母表的符号。

字母表上的字符串为该字母表中符号的有穷序列，不用逗号隔开。

比如$\Sigma={0,1}$，则$0110$为其上的一个字符串，简称串。长度为0的串称空串，记作$\varepsilon$.

对字符串有连接和翻转两种运算。串连接有单位元$\varepsilon$。

字符串的集合称为语言，可表述为：

\[A\in\Sigma^*:=\{\varepsilon,0,1,00,01,10,11,...\}\]

排列顺序为：字典序+长度=标准序；

其上的星号运算可以理解称由字母表生成语言，如：

\[B^*:=\{x_1x_2...x_n\mid x_1,...,x_n\in B,n=0,1,...\}\]

对语言$A$有多种操作：

1. 定义其幂集，$P(A);2^A$
2. 笛卡尔积，自然定义
3. 连接操作，指把两个集合中的字符串一一连接。
4. 空集合，又称空语言，是语言连接的零元
5. 空串语言${\varepsilon}$，是语言连接的单位元。

1 确定性有穷自动机

计算理论的第一个问题是，什么是计算机？或许你手里就有一台电脑，你说，这就是计算机。但现实的计算机往往十分复杂，为了进行数学上的研究，我们构建“计算模型”。同物理中的模型一样，一个计算机模型精确地刻画了某些特征，但也忽略了部分细节。

本节从最简单的计算模型开始，它称为有穷状态机，或者有穷自动机。根据转移函数的确定性，可分为确定型有穷自动机(deterministic finite automata DFA)，非确定有穷自动机(NFA).

1.1 DFA的形式化描述

DFA为一个五元组：$(Q,\varSigma,\delta,q_0,F)$，其中

1. $Q$是有穷状态集；
2. $\varSigma$为有穷字母表；
3. $\delta:Q\times\varSigma\to Q$为转移函数；
4. $q_0\in Q$是起始状态；
5. $F\subseteq Q$是接受状态集.

除了五元组外，还有状态转移图和状态转移表两种描述方式，一种很直观；另一种也很直观。

1.2 例子

若$A$是机器$M$接受的全部字符串集(一个充分必要关系)，则称$A$是机器$M$的语言，记作$L(M)=A$.又称$M$识别或者接受$A$

• 定义，如果一个语言被一台DFA识别，那么称它为正则语言（Regular Language）。

例1：$A_1= { 0^n1^m\mid n,m\ge 0 }$

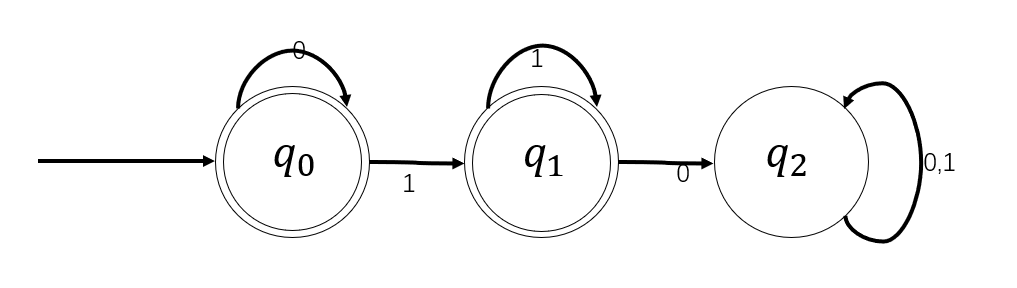
考虑另一个情况$A_2={1^n0^m\mid n,m\ge 0}$

例2：$A_3:=A_1\cap A_2={0^n,n\ge 0}\cup{1^m,m\ge 0}$

例3：$A_4:=A_1\cup A_2={0^n1^m\mid n,m\ge 0}\cup{1^n0^m\mid n,m\ge 0}$

这两个例子的DFA也可以很快地画出来：

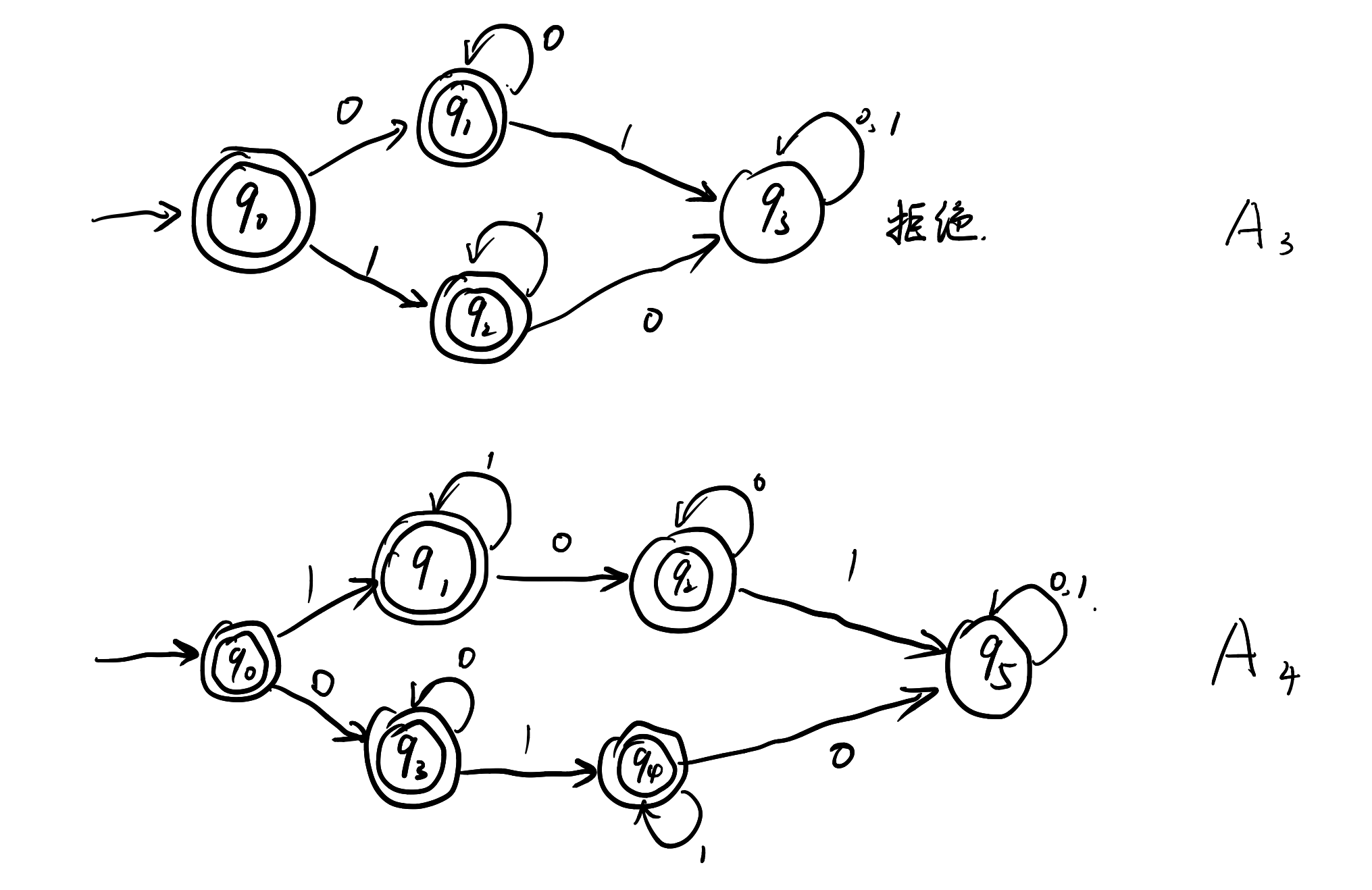
但对于$A_4$这个对应的DFA来说，有没有一种可能，将它的状态变得更少一点？

这涉及到自动机里面一个十分重要的定义，就是等价状态。如果两个状态之间等价，那么两状态就可以化成一个状态，从而实现了简化。

1.3 等价状态

首先，为了方便起见，我们扩展转移函数的定义，使它一次可以接受一个字符串而不是单个字符。

\[a\in\Sigma,x\in\Sigma^*,\qquad \delta'(q_1,ax):=\delta'(\delta(q_1,a),x)\]

如此，我们就可以方便地定义两个状态之间的等价。

\[\forall x\in\Sigma^*,\forall q_1,q_2\in Q，if\ \delta'(q_1,x)\in F \iff \delta'(q_2,x)\in F\]

我们就称$q_1,q_2$两状态等价。这说明对于任何一个输入串，两状态的行为均是一致的。

不等价状态就是其否命题，若存在一个字符串，使得一个处于接受状态，一个处于拒绝状态即可。

由此可以延伸出一种区分算法，和离散数学课上的Graph Partition算法十分相像，只需要选取$F,\bar F$作为划分即可，每次按照一个字符读入区分。

$F$		$\bar F$
$q_1$	$q_2$	...	...

如此一层层往下，只要读入$0，1$能够分开，就把它们分开。如若不行，就作为一格下次再来区分。

对于DFA来说，考虑最坏的情况，也就是每个状态之间都是两两区分的(也就是不等价)，则最多步数为$\mid Q\mid ^2$，即可完成。

此外，还有一个定理叙述了相同的事情：

• Myhill-Nerode定理：$L=L(M)$，则可定义二元关系，不可区分$\sim_L$。此关系为等价关系，若$x\sim_L y \iff {\forall z\in L, xz\in L \quad iff\quad yz\in L}$

根据这个等价关系可以给DFA图一个划分，从而得到最小状态集。此外，还可以定义$L$的指数为用$L$两两可区分的集合中的元素个数的最大值。这个指数的有穷性表述了该语言是否是正则语言。

根据我们扩充的转移函数的定义，可以得到$x,z$本质上就是一个状态，因为自动机的入口是确定的，而转移也是确定的。所以这个定理和前面的算法都可以完成最小状态的划分。但是后者的威力不仅限于此，它还可以作为正则语言的判断。从这里，我们已经可以看到语言和自动机密不可分的关系。在图灵机中，我们还会定义格局的概念，和此处极为相似。

1.4 正则运算

本小节讲述对于语言的运算操作。定义语言的三种运算，称为正则运算（regular operation）

• 设$A$和$B$是两个语言，定义正则运算并、连接和星号：
• 并：$A\cup B={x\mid x\in A\ or\ x\in B }$
• 连接：$A\circ B={xy\mid x\in A \ and\ y\in B}$
• 星号：$A^*={x_1x_2…x_n\mid x_1,…,x_n\in A,n\ge 0}$

关于star运算，我们可以写成$A^*=A^0\cup A^1\cup A^2…$，其中定义
$A^0={\varepsilon},A^k=A\circ A\circ…$k个

接下来我们证明正则语言在上述三种运算下是封闭的。(事实上还有其他运算)

• 正则语言类对并运算封闭

证明：此时我们只有定义，所以只能构造DFA来证明。

核心思想为，既然并运算是或关系，那么我们只需要扩展状态集合，使其称为一个二元组。如：

\[Q'=Q_1\times Q_2\]

同时扩充转移函数和接受状态集即可。只需要一个达到接受状态，即可接受。这里需要形式化表述一下接受状态集的构造:

\[F'=(F_1\times Q_2)\cup(F_2\times Q_1)\]

即可证毕。

• 正则语言类对补运算封闭

证明：只需要翻转接受状态即可。

当然，这个证明会可以因为扩充转移函数的定义而更加清晰。

即可证毕。

• 正则语言类对交运算封闭

证明：由德摩根律，我们可以知道交运算可以由补和并生成。这两个运算是封闭的，那么组合起来也是封闭。

另外，我们也可以模仿对并运算的证明。同样扩充状态集合和转移函数。但是交运算的核心是同时，所以对此时接受状态集合的构造为：

\[F'=F_1\times F_2\]

也就是需要同时被两种语言接受。

即可证毕。

• 正则语言类对连接运算封闭

证明：由于这个证明需要对两个语言的两台自动机说明，所以需要形式化表述一下。对于语言$A\circ B$，第一台DFA是$M_1$，接受语言$A$；而$M_2$接受$B$。

连接运算的核心是$M_1$接受前面的串，然后由$M_2$接受后面的串。但是我们无法确定到底是从哪一个字符开始分割前后。所以需要构造记录这一时刻的DFA。

也就是，当$M_1$接受时，启动一台$M_2$，此时$M_1$仍然需要执行下去。鉴于$M_2$多台启动的可能性，于是对状态集扩充：

\[Q'=Q_1\times P(Q_2)\]

此时对于初始状态也就有一点讲究了。如果$M_1$的的初始状态就接受，那么一开始就要启动$M_2$，所以起始状态为：

\[q'=(q_1,\{q_2\})\]

否则就是:$ q’=(q_1,\emptyset) $

而对于转移函数来说，问题就在于反复启动的机器$M_2$。此时，需要实时判断转移后的第一个状态是否在$M_1$的接受状态$F_1$，如果在就像后面的状态子集中加入一个$q_2$，否则不需要加入。

最后考察接受状态，也就是最后$q=(q_i,{q,..})$的状态，只需要后面的集合与$F_2$交非空即可。

即可证毕。

这种构造已经表现出一点非确定性的思想在里面了。所谓非确定性，也就是猜。

• 正则语言类对于星号运算封闭

证明：考虑星号运算的展开，即可证毕。需要注意的是，星号运算所产生的语言集合中的字符串都是有穷长度的。所以才能由连接和并运算保证星号运算的封闭性。

当然，我们也可以构造自动机证明。

构造过程类似于连接，只不过其中$M_2$就是$M_1$，而且只需要有一个状态处于接受状态中即可。

综上证毕。

2 非确定性有穷自动机

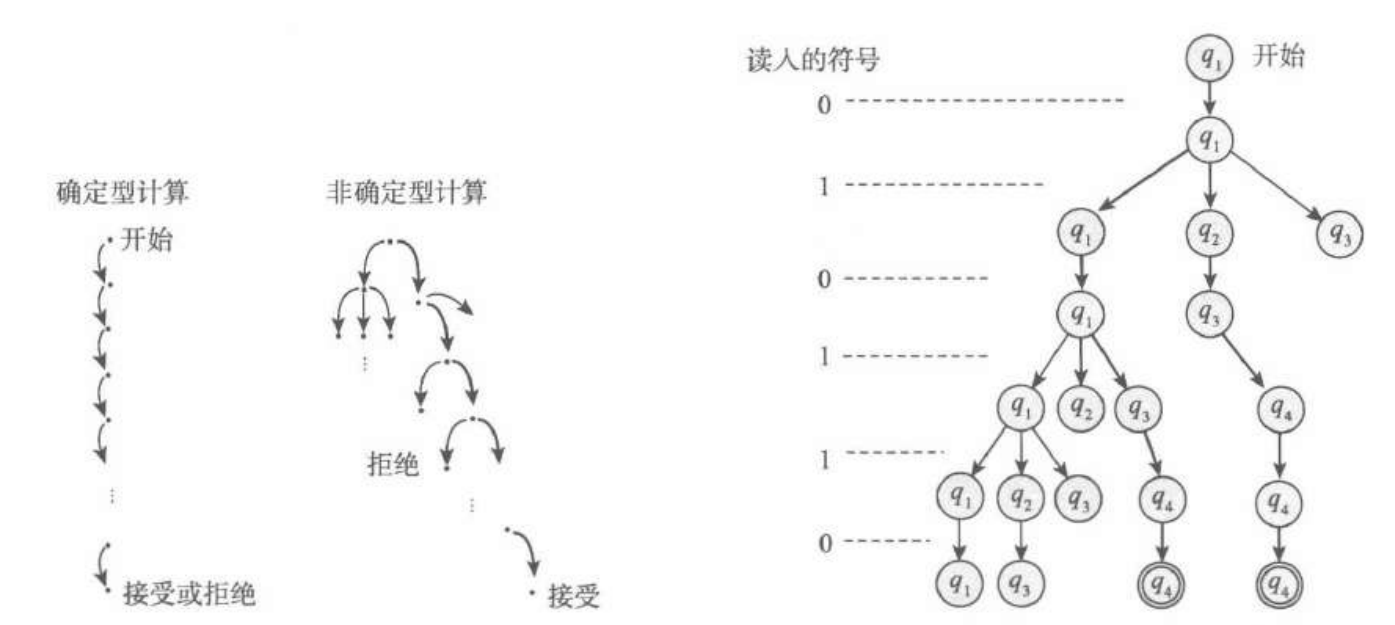
所谓非确定计算，也就是随时刻产生不同的备份，当备份无法移动时消逝；如果有一个备份计算状态到达接受状态，那么整个机器就接受。非确定型有穷自动机简称NFA。

2.1 简单的例子与介绍

字母表仍然取$\Sigma={0,1}$.

考虑语言$N_1$，其为倒数第三个字母是1的那些字符串集合。

对于NFA来说，只需要猜测就行了，如果读到一个1，那么我就可以猜这就是倒数第三个，然后读三个数，如果是就解决，否则直接删备份。而对DFA来说，就不得不采用8个状态记录读下的三个字符。两自动机如下：

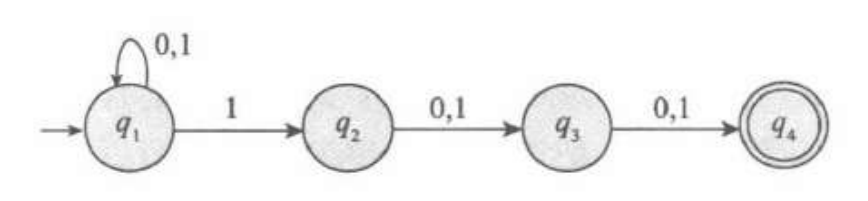
DFA

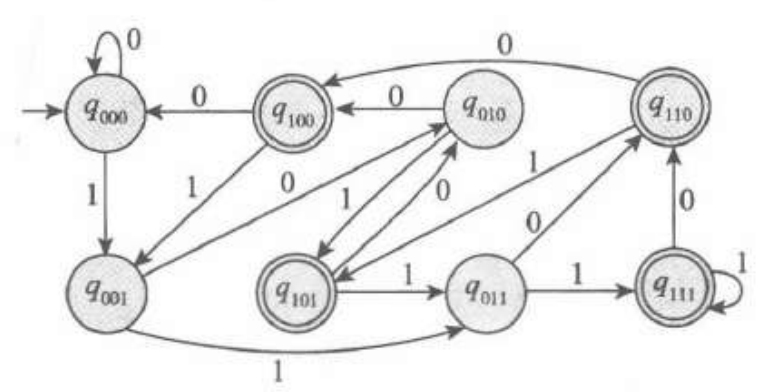
2.2 NFA的形式化定义

NFA也是一个五元组：$(Q,\varSigma,\delta,q_0,F)$，其中

1. $Q$是有穷状态集；
2. $\varSigma$为有穷字母表；
3. $\delta:Q\times\varSigma_\varepsilon\to P(Q)$为转移函数；
4. $q_0\in Q$是起始状态；
5. $F\subseteq Q$是接受状态集.

NFA读入字符串$\omega$可生成一串状态序列，如果其首状态起始，末状态与接受状态集交非空，则接受串$\omega$.

综合来看，NFA计算的过程是这样的：

2.3 NFA与DFA的等价性

尽管非确定性看起来十分的强大，可以对状态个数做极大的优化，但是并不能扩大计算的范围。我们定义等价的概念：

• 如果两台机器识别同样的语言，则称它们是等价的。

非确定性扩大了计算的能力，在图灵机时，我们就可以看到非确定性对于计算能力的提升。从中可以定义$NP$难的问题。但是这种非确定性对于实际计算机涉及并没有太多的借鉴意义。

• 定理：每一台NFA都等价于一台DFA

证明： 从定义上来看，NFA可以完成DFA计算，这一方向十分的简单。所以主要是讨论用DFA模拟NFA，或者将NFA转化成一台DFA。

大致思路和RL对连接运算封闭的证明一致，也就是通过构建子集来记住每一时刻NFA的状态；不过还需要引入闭包的概念，这是为$\varepsilon$移动准备的。

这个概念是从NFA中消除$\varepsilon$移动的核心。也就是定义：

\[E(R):=\{q\mid 从R触发，沿着若干个\varepsilon可以到达的q\}\]

借此修改转移函数，也就是用$E\delta$的合成代替$\delta$。注意合成运算的顺序，很多时候就是这种小地方引起的失误。

综上可知证毕

接下来，我们举一个实例：

对于下面这个NFA：

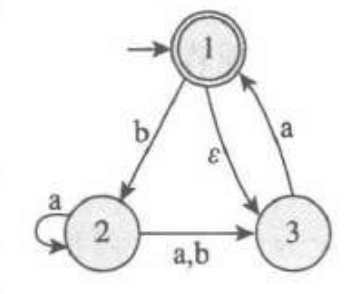
先构建幂集，如下，然后确定闭包。最后对每一个状态考虑转移函数$E\delta$.

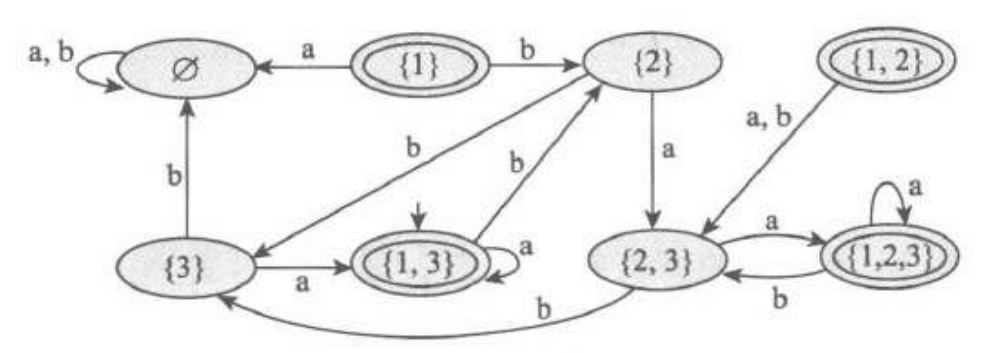
最后消去那些只出不进的状态，就完成了。

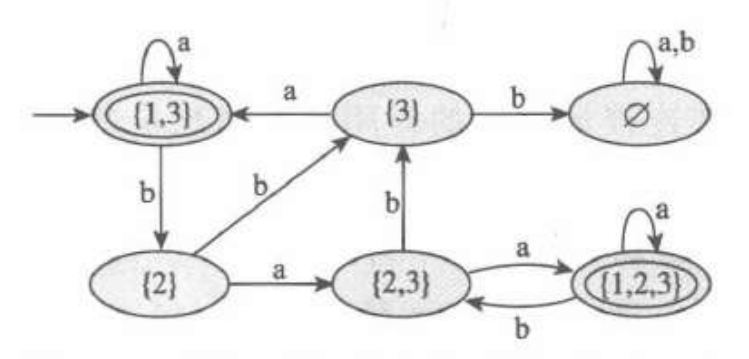
不同的是，NFA没有可区分性这个概念。

2.4 RL封闭性的新证明

有了非确定性的概念和等价性，我们知道一个语言能被NFA识别，就能被DFA识别，就是一个正则语言。

• RL对并封闭

重新创建一个初始状态，按$\varepsilon$移动进入两台DFA；需要注意初始状态读入非空字符直接消除备份。

• RL对连接封闭

对于第一台DFA的接受状态，直接$\varepsilon$移动进入第二台DFA

• RL对星号封闭

这里简单想，就是把接受状态直接$\varepsilon$移动到初始状态，但是需要注意的一点是，$\varepsilon$也在其中。所以需要重新创建一个初始状态，然后再进入原来的初始状态。

3 正则表达式

到此为止，我们已经有了两种方式描述正则语言，分别是DFA和NFA。但是我们只是通过计算接受的方式考虑它，并没有很好的直观认识。接下来我们用正则表达式（Regular Expression or REX）来直观地描述它。

3.1 形式化定义和一些约定

我们可以用正则运算符来构建正则表达式。其中，我们约定用元素的形式来表达集合，比如${0}$可以用0来表达，也就是$(0\cup1)$代表${0,1}$；此外，连接符号通常会被省略。

运算的优先级为$*>\cup > \circ$。接下来，我们给出形式化归纳定义：

• 称$R$是一个正则表达式：
• $a，a\in \Sigma$
• $\varepsilon$
• $\emptyset$
• ($R_1\cup R_2$)
• $(R_1\circ R_2)$
• $(R_1^*)$

我们称正则表达式$R$表达的语言为$L(R)$

正则表达式与编译过程中的词法分析器紧密相关。比如一个数字可以描述为：

\[(+\cup-\cup \varepsilon)(D^+\cup D^+.D^*\cup D^*.D^+)\]

这里’.’运算的优先级高于并运算

另外，用正则表达式表示语言也很方便。比如倒数第三个字符为1的语言为：

\[(0\cup1)^*1(0\cup1)(0\cup1)\]

3.2 REX与DFA的等价性

• 首先证明由REX生成DFA，我们只需要按定义一步步生成即可。

其生成过程和用NFA证明RL封闭一致

• 比较困难的一遍是用DFA生成REX

一个常用的证明方法是使用GNFA，也就是广义非确定性有穷自动机。

它可以直接读入REX，而不是仅仅为字符串。但是引入它的证明是繁琐的。而且对于应用来说是没必要的。所以我们直接描述大致的运算过程。随后给出GNFA的相关概念和信息

核心就是利用这种广义性，来完成第一段证明的反过程。通过对某一个状态的删除， 从而将其上的多条转移变成一条转移。直接上图：

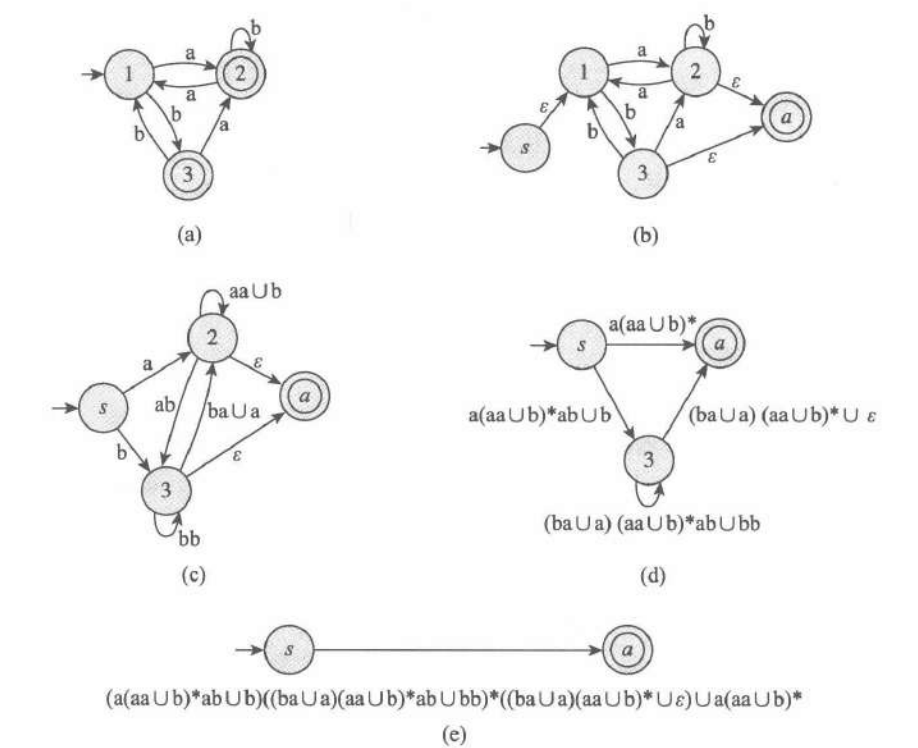
3.3 GNFA

4 非正则语言

根据辩证法的指引，我们还需要对非正则语言有一个大致的了解，才能更好地理解正则语言的能力与局限。

回顾之前的讨论。我们已经可以用DFA、NFA、REX来描述正则语言了。接下来，我们将使用一个必要条件和一个充分必要条件来描述REG，后者还可以给出一个最小自动机的构造方法。

4.1 泵引理

考虑一个DFA M，其接受串$x_1x_2…x_n\in L(M)$。

则有状态序列：$q_0q_1…q_n$。如果$n\ge \mid Q\mid$，由鸽巢原理得到序列中必有两个状态对应同一个DFA状态。设为$q_i,q_j$，则可将状态和字符串拆分为

\[q_0\stackrel{x}{\longrightarrow}q_i\stackrel{y}{\longrightarrow}q_j\stackrel{z}{\longrightarrow}q_n\]

其中$y$是可以任意加入或者抽出的，这就是泵引理。

下面给出一般表述：

• 泵引理：$\forall L\in REG，\exists p>0$称为泵长度。使得$\forall s\in L$，若$\mid s\mid \ge p$，则有$s=xyz$满足：
  • $\mid xy\mid \le p$
  • $0<\mid p\mid\le p$
  • $xy^iz\in L$

该定理作为正则语言的必要条件，大多用来证明非正则语言。而且使用反例构造，下面给出粒子。

例4：$L_1={0^n1^n\mid n\ge 0}$

若是，考虑泵长度$p$下的$s=0^p1^p$。

其长度超过$p$，由泵引理可知$y$为全零串，那么增减必然失衡，矛盾证毕。

此外，如果对正则语言类熟悉的话，还可以用封闭性证明。

比如$L_2= { x\mid x\in{0,1}^*,\mid x\mid_0=\mid x\mid_1 }$

有$L_2\cap 0^1^=L_1$，由封闭性知不可能。

REG对Reverse也是封闭的。

例5：$L_1={ww\mid w\in{0,1}^*}$

这类语言称为上下文有关语言。

如果其为正则语言，同样设$0^p10^p1$即可。

例6：$L_1={0^i1^j\mid i<j}$

取$s= 0^p1^{p+1}$，然后增加。

4.2 Myhill-Nerode定理

• 定义等价关系$\sim_L$:
• $\forall z\in \Sigma^*, xz\in L, yz\in L$同时在或者同时不再，称为不可区分关系。
• 这样，我们就得到$\mid \Sigma^*/\sim_L\mid< \infty$是$L\in REG$的充分必要条件。

证明的核心思想是，通过对于$L$字符串和自动机状态的一一对应关系。对于初始状态来说，读入一个等价类的字符串，应该到达一个新状态。然后根据这个新状态读入即可。