前一篇描述了正则语言的描述方法,但是他并不能描述所有语言,比如01等的情况。 本章介绍一种能力更强的描述数学语言的模型,称为上下文无关文法。它能够描述某些应用广泛的具有递归结构特征的语言。
1 上下文无关文法 CFG
所谓文法,就是一定的规则。比如主词后面跟谓词,诸如此类的规则。
我们直接给出形式化定义
1.1 CFG的形式化定义
- CFG是一个四元组:$(V,\varSigma,R,S)$
- $V$是一个有穷集合,称为变元集;
- $\varSigma$是一个与$V$不相交的有穷集合,称为终结符集;
- $R$是一个有穷规则集。规则由一个变元和一个由变元和终结符组成的字符串构成;
- $S\in V$是起始变元。
比如有规则:
\[A\to \alpha\]那么有:
\[xAy\Rightarrow x\alpha y\]其生成与$x,y$无关,故称为上下文无关。上述过程称为派生,多个*成多步派生。
派生的逆过程称为归约。
另外,由于对于一个CFG来说,只有规则集是必不可少的,其它或多或少都可以由规则集看出。故每次书写只表示规则集。
例1::$L_1= { 0^n1^1\mid n\ge 0 }$
有文法:$G_1:S\to \varepsilon\mid 0S1$
由此可以产生一个语法分析树:
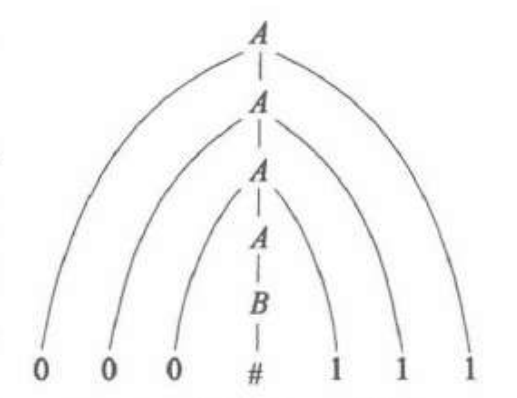
值得一提的是,文法的设计十分需要创造力。
1.2 歧义性
但是对于同一个表达式,可能会有多种语法分析树。我们考虑最左派生,如果一个文法针对同一个字符串有两个以上的最左派生,则称文法歧义地生成这个字符串。如果文法能够歧义地生成某个字符串,那就称文法是歧义的。
比如文法:
\[G_2:E\to E+E \mid E\times E\mid (E)\mid a\]上述文法产生$a+a\times a$就是歧义的,这对于语法分析来说是毁灭性的灾难。因为我们无法确定加减的顺序。
- 有的语言的歧义性可以消除,但是部分语言的歧义性是无法消除的,这类称为固有歧义语言。
比如语言:${0^n1^n2^m\mid n,m\ge 0}\cup{0^n1^m2^m\mid n,m\ge 0}$
左侧可有文法:
\[S_1\to AB\\ A\to 0A1\mid \varepsilon \\ B\to 2B\mid \varepsilon\]右侧:
\[S_2\to CD\\ C\to 0C\mid \varepsilon \\ D\to 1D2\mid \varepsilon\]所以可以生成$G:S\to S_1\mid S_2$
考虑语言${0^n1^n2^n\mid n\ge 0}$,它必然会有两种最左派生。当然,它可能也不属于CFL。
从上文可以看出,CFL对交不封闭,但对并封闭。此外,它还对*,连接封闭
1.3 乔姆斯基范式
对于一个文法来说,它生成的所有串的集合称为这个文法对应的语言。
那么如何判断这个串属于这个语言呢?也就是$\forall w,G,x?\in L(G)$
显然,文法的生成是无止尽的,我们很难得到一个确切的生成顺序。但是乔姆斯基范式–CNF可以帮我们完成这个难题。
- CNF规定
- 只有初始变元能生成空字符,而且没有任何变元能生成起始变元;
- 任何一个变元,它要么生成两个变元,要么生成一个终结符号。$A\to BC\mid a$
如此,我们就可以对给定长度$n$的字符串做派生,而且必然在$\lceil n/2 \rceil$步内生成.
接下来我们讲述这个算法:
用$S\to SS\mid (S)\mid \varepsilon$做示范。
- 引入新的初始变元$S_0$,从而保证起始变元不出现在右侧
- $S_0\to S,S\to SS\mid (S)\mid \varepsilon$
- 对于将$\varepsilon$生成交给起始变元,并且把$A\to \varepsilon$删除。然后对于所有右侧的$A$均用空字符替换,保留所有可能性
- $S_0\to S\mid \varepsilon,S\to SS\mid (S)$
- $S_0\to S\mid \varepsilon,S\to SS\mid S\mid (S)\mid ()$
- $S_0\to S\mid \varepsilon,S\to SS\mid (S)\mid ()$
- 删除变元单一规则$A\to B$,将B的派生归入A
- $S_0\to SS\mid (S)\mid ()\mid \varepsilon,S\to SS\mid (S)\mid ()$
- 对多元派生做左线性化,引入中间变元完成
- $S_0\to SS\mid (S)\mid ()\mid \varepsilon,S\to SS\mid (S)\mid ()$
- $S_0\to SS\mid (S)\mid ()\mid \varepsilon,S\to SS\mid (S)\mid (),L\to (,R\to ),T\to SR$
- $S_0\to SS\mid LT\mid LR\mid \varepsilon,S\to SS\mid LT\mid LR,L\to (,R\to ),T\to SR$
完成。这种处理最后得到的CNF不是唯一的。
所谓左线性化,就是$1\to 11$,这样依次增多的生成;右线性化则是变少。
借助这个概念,我们很容易证明:$REG\subseteq CFG$
对字符串$x_1…x_n$,依次有状态$q_1..q_n$接受,则构造CFG:
\[q_i\stackrel{a}{\longrightarrow}q_j\\ q_i\to aq_j \iff \delta(q_i,a)=q_j\]最终为:
\[q_0\Rightarrow x_1q_1\Rightarrow x_1x_2q_2 ...\\ q_0\stackrel{*}{\Longrightarrow} x_1...x_n\]2 下推自动机 PDA
所谓下推自动机,就是一种利用栈的计算模型。相对于DFA而言,多了额外的一个无限的存储空间,所以计算机能力强了很多。比如之前的01语言,就压入0,读到1便弹出,如此便可完成识别。
2.1 形式化定义
- PDA是一个六元组:$(Q,\varSigma,\varGamma,\delta,q_0,F)$:
- $Q$是有穷状态集;
- $\Sigma$是输入字母表;
- $\Gamma$是栈字母表;
- $\delta:Q\times \Sigma_\varepsilon\times\Gamma_\varepsilon\to P(Q\times\Gamma_\varepsilon)$是转移函数;
- $q_0\in Q$是起始状态;
- $F\subseteq Q$是接受状态集合。
然后我们使用$号表示栈底。
这里我们需要叙述一下转移函数的$\varepsilon$移动:
- $\delta(p,\varepsilon,\varepsilon)$,双$\varepsilon$移动;
- $\delta(p,\varepsilon,x)$,$\varepsilon$输入移动;
- $\delta(p,a,\varepsilon)$,$\varepsilon$栈移动;
- $\delta(p,a,x)$,非$\varepsilon$移动。
DPDA有且仅有一种移动的可能。
另外,关于PDA的四种行为:不动;替换;弹出;压入。我们只需要讨论后两者即可,后两者是完备操作集。
接下来给出01的例子:
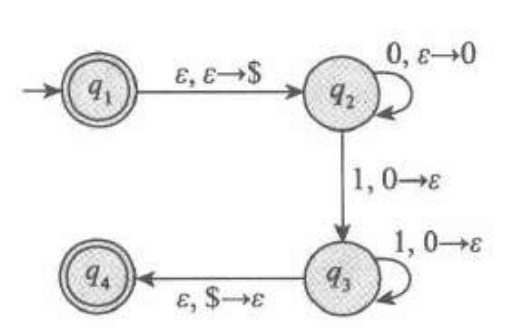
| 输入 | $0$ | $1$ | $\varepsilon$ | ||||||
| 栈 | $0$ | $\$$ | $\varepsilon$ | $0$ | $\$$ | $\varepsilon$ | $0$ | $\$$ | $\varepsilon$ |
| $q_1$ | $\{(q_2,\$)\}$ | ||||||||
| $q_2$ | $\{(q_2,0)\}$ | $\{(q_3,\varepsilon)\}$ | |||||||
| $q_3$ | $\{(q_3,\varepsilon)\}$ | $\{(q_4,\varepsilon)\}$ | |||||||
| $q_4$ | |||||||||
2.2 非确定性
为了更好的描述PDA的计算,我们定义格局。它是用来描述PDA当前状态的。
- 格局:$(q,u)\in Q\times \Gamma^*$。有初始格局:$(q_0,\varepsilon)$
于是我们可以描述上述PDA读入000111的行为了。
此外我们还可以定义接受格局,和初始格局类似。以空栈为接受格局的PDA接受前缀无关的语言。当然,我们可以直接给任何语言加上一个结束符,那么就消除了前缀无关。
对于两种接受格局,PDA是无所谓的;但是DPDA有区别,显然空栈会弱一些。
PDA 的非确定性来自于文法的歧义性,也来自于CFL的不确定性。
一个例子是${0^n1^n}\cup{0^n1^{2n}}$;
或者${0^n1^n2^m\mid n,m\ge 0}\cup{0^n1^m2^m\mid n,m\ge 0}$
2.3 CFL$\iff$PDA
这一小节,我们证明CFL与PDA等价。
- CFL$\to$PDA
证明核心在于构造一台PDA,
我们给出三个核心状态:$q_{accept},q_{loop},q_{start}$
这里暂时只给一种方式派生-弹出,又称自底向上处理法分析树
- 从$q_{start}$开始读入初始变元;
- 然后进入$q_{loop}$,考虑弹出变元进入一个新状态,随后压入规则的右侧;
- 弹出终结符,直到变元出现,根据规则如此往复。
- 空栈弹出$
还有另外一种办法,为移进-归约,又称自顶向下处理法分析树。但还需要一种DK-测试的手段。
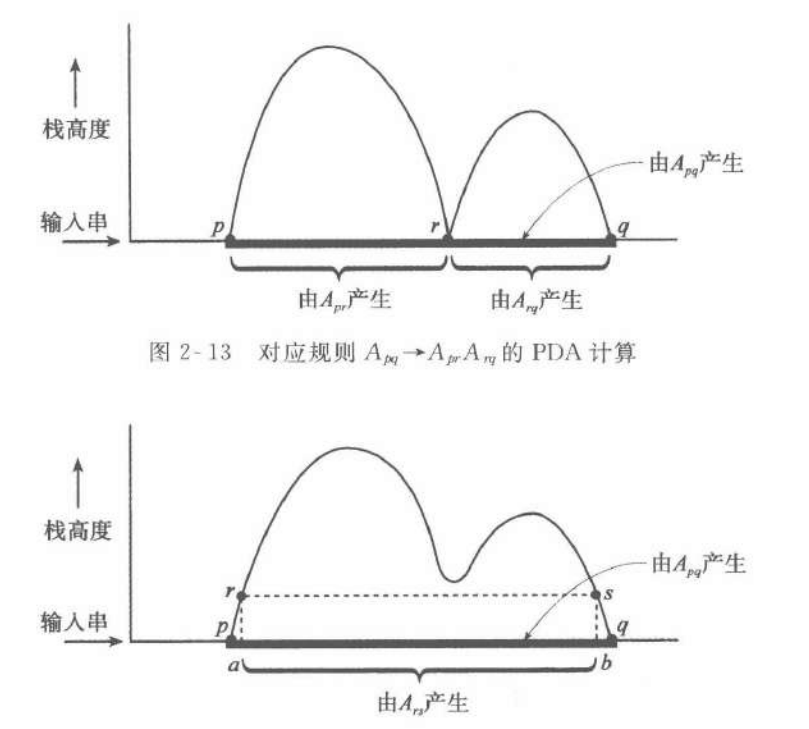
- PDA$\to$CFL
这里的证明需要对PDA做一些约定:
- 只有唯一的初始状态和接受状态;
- 每步必须有变元弹出或者压入;
- 接受时空栈。
那么只需要对下图做归纳即可。
3 CFL的泵引理
考虑任意一个CFG,对其任意一条规则:
\[A\to \alpha\]令$b=\max\mid \alpha\mid$,即所有语句中一次生成最多的变元个数。
考虑$\mid V\mid+1$层生成树,由鸽巢原理得到必有两个点,生成变元相同。类似于RL的泵引理,我们可以替换或者增减,它仍然是属于该CFG的。(R为最下层的重复变化)
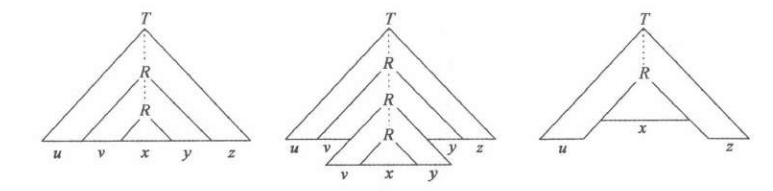
这就得到了CFG的泵引理:
- 对$L\in CFL$,$\exists$泵长度$p=b^{\mid V\mid +1}$,若$\mid s\mid\ge p$:
- $s=uvxyz$
- $\mid vxy\mid \le p$
- $\mid vy\mid >0$
- $uv^ixy^iz\in L$
它仍然只是一个必要条件。
比如对语言${0^n1^n2^n\mid n\ge0}$
取$s=0^p1^p2^p$,分析即可。
对比如对语言${0^i1^j2^k\mid i\ge j\ge k\ge0}$同理。