之前的讲述都不过是热身,到了这一章,计算理论才显现出真正的威力。
1 图灵机
图灵机有一个无穷长的表带,一个可以在表带上移动的读写头。
1.1 定义
图灵机是一个七元组 ${Q,\varSigma,\varGamma,\delta,q_{0},q_{accept},q_{reject}}$,其中$Q,\varSigma,\varGamma$都是有穷集合:
- $Q$是状态集。
- $\varSigma$是输入带字母表,不包括特殊空白符号$B$。
- $\varGamma$是带字母表,其中$B\in \varGamma$,$\varSigma \subset \varGamma$
- 转移函数$\delta : Q \times \varGamma \to Q \times \varGamma \times {\to, \gets }$
- 起始状态$q_{0}\in Q$
- 接受状态$q_{accept}\in Q$
- 拒绝状态$q_{reject}\in Q$,且$q_{accept}\neq q_{reject}$
图灵机与之前的计算模型相比,有几点特殊之处:
- 只有唯一一个接收状态
- 可以任意地回溯和读写
- 可以不读完输入就直接判断
如果是单侧无穷长,可以像栈一样加一个符号作为标志。
针对语言${0^n1^n2^n\mid n\ge0}$,可有图灵机:
- 算法:
- 检查输入是否为$0^{}1^{}2^{*}$
- 检查0,1,2个数是否相等。
算法是对图灵机的高层描述,而不纠结于细节。
- 实现:
- 从左往右扫描输入,用状态记录看到的输入
- 从左往右扫描输入,配对消去0,1,2;如果恰好都消去,则停机接受,否则停机拒绝。
这里我们不再给出它的状态转移图或者状态转移表,这不再是我们接下来的重点。我们会更加关注前两种描述。
此外,对于图灵机的计算,我们定义为一系列格局(Configuration)。
所谓格局,就是对当前状态和带内容的记录:
\[uqav\qquad u,v\in\Gamma^*,a\in\Gamma,q\in Q\]$a$为读写头当前所指状态。格局的序列称为图灵机的计算。显然,我们有:
- 存在初始格局:$q_0w$;
- 格局的转换$C_i\to C_{i+1}$,符合转移函数;
- 最后一个格局为停机格局。
1.2 变种
所谓变种,没有什么本质区别。
比如多带、双向无穷带,哪怕多个指针独立运动。单侧无穷带都可以模拟。
这是由可数集合的势保证的。
具体的实现手法倒是许多,比如分段、分道等。
另一种比较有意思的变种是非确定性的计算树。由于多带的等价性,我们可以使用一条输入带记录,另一条01带用来枚举选择。如此也可以模拟。(广度优先)
对于可计算性来说,这些变种都没有本质区别;但是对于计算复杂度来说,则天差地别。
1.3 丘奇-图灵论题
历史上有三种对计算的定义,它们都是等价的。
分别是递归函数论、$\lambda$演算、图灵机。由于自它们提出以来,没有计算性更强的描述出现,所以选择形式上最简单的图灵机作为计算的定义。
由于无法对所有计算模型做考察,所以目前还只是一个论题。可计算性理论正是依托此定义构建的。
对于图灵机接受的语言:$L(M)={x,\mid x\in \Sigma^*,q_0x能进入接受格局中}$。
在其上,我们可以对问题进行分类。
- 图灵可计算/可判定问题:
- $x\in L$,则必存在一个接受计算;
- $x\notin L$,则必存在一个拒绝计算。
这些问题也称为处处停机问题。
- 图灵半可计算/可识别问题:
- $x\in L$,则必存在一个接受计算;
- $x\notin L$,则必存在一个拒绝计算或者不停机。
- 补图灵可计算/可识别问题:
- $x\in L$,则必存在一个拒绝计算或者不停机;
- $x\notin L$,则必存在一个接受计算。
我们还可以定义出TM的计算函数:
\[f:\Sigma^*\to\Sigma^*,x\mapsto f(x)\]即为停机带上的输出。
1.4 TM的表示
在这之前,我们已经见过一些描述了。
-
形式化描述:七元组;状态转移图(表)
- 实现描述:
- 如何处理数据;
- 带头如何移动。
- 高层描述:TM $M=$”对于输入$x$”
- 如何如何
- 如何如何
- …..
比较重要的一种描述是编码: $\langle M\rangle$
他能够将图灵机的描述转换成具有一定结构的字符串,这种转换在知道规则的情况下可逆。
后面我们还会介绍通用图灵机$U(\langle M\rangle,x)$,它能够模拟$x$在M上的输入情况。
2 可计算性
关于可计算性的分类,前面已经有过阐述。这里只是举一些例子,并给出其间的一些关系。
2.1 一些实例
- 定理2.1.1: 语言$L$可判定$\iff$$L,\bar L$都是图灵可识别的。
一个简单的事实是,$L$是图灵可识别的,当且仅当其补语言是补图灵可识别的。
那么接下来就很明晰了。从左推右按定义即可;右推左使用$\varepsilon$移动,非确定地进入两个图灵机即可。
构造的核心在于避免停机的情况。也就是说,两个图灵机你一步我一步,防止一个图灵机直接进入死循环。
- 图灵机接受性问题:
- 输入:TM M,串 x;
- 输出是/否,是则$x\in L(M)$;否则$x\notin L(M)$。
我们可以把整个问题转化成语言判定的问题:
\[A_{TM}=\{\langle M,x\rangle\mid TM,M接受x\}\]而完成这一过程的称为通用图灵机$U(\langle M\rangle,x)$,我们只需要对M做解码即可。
如果M接受,那就接受;拒绝则拒绝,不停机则不停机。所以是图灵可识别语言。
接下来我们对$A_{TM}$,考虑它是不是一个可判定语言。
使用的方法是一个著名的对角化方法,在许多逻辑学的证明中都会用到。
2.2 对角化方法
首先,我们考察TM的所有编码,那么$\Sigma^*$中存在着所有的图灵机编码,为了方便于我们讨论,我们将那些不完善编码的图灵机记作$M’$,它们直接停机。
- 定理2.2.1:$A_{TM}$不可判定。
我们用反证法,考虑一个TM H,它能够接受一个图灵机的编码和一个串:
\[H(\langle M\rangle,x)\]其结果就是模拟串x在图灵机M上的结果。但是H能够直接判定,这个串是否被接受,而没有停机的情况。
接下来我们考虑编码,由于$\Sigma^*$是可数集,那么所有的图灵机是可枚举的,那么算法、也就是处处停机的图灵机也是可数的。
如此,我们就枚举所有的图灵机并考虑:$H(\langle M_i\rangle,\langle M_i\rangle)$
| $ |
$ |
$ |
$ |
$ |
$ |
… | |
|---|---|---|---|---|---|---|---|
| $M_0$ | 1 | ||||||
| $M_1$ | 0 | ||||||
| $M_2$ | 1 | ||||||
| $M_3$ | 0 | ||||||
| $M_4$ | 1 | ||||||
| $M_5$ | 1 | ||||||
| … | … |
这里需要注意的一点是,串$\langle M_i\rangle$是作为单纯的串而言的,而不需要考虑其对应的图灵机内容。我们可以直接令$x_i=\langle M_i\rangle$,那么就是考虑图灵机$H(\langle M_i\rangle,x_i)$。这样可能更加清晰。
接下来,利用这个对角线,我们再构造一个图灵机$D$,它的行为是:
- 对于输入$\langle M_i\rangle$,我们模仿$H(\langle M_i\rangle,x_i)$,不过我们对其结果取反。也就是H输出接受1,那么D就输出0.
这样,我们就得到一个这样的图灵机D,它相对于图灵机$M_i$,在串$x_i=\langle M_i\rangle$上有着不同的输出。那么依照无穷的对角线,我们构造了一个不在其中的图灵机。这自然构成矛盾。
进一步,我们指出:
- 若图灵机D接受串$\langle D\rangle$;
- 则图灵机H拒绝串$\langle D\rangle$;
- 则根据H的定义有$(D,\langle D\rangle)\in A_{TM}$;
- 根据$A_{TM}$的定义,图灵机D不接受串$\langle D\rangle$。
- 矛盾。
2.3 kleene范式定理
- $L$可识别$\iff L={x\mid \exist y, \langle x,y\rangle \in C}$。其中C是可判定语言。
证明:
右推左:构造一个图灵机,给出高层描述:
- 对于输入$x$;
- 枚举字符串$y$,由于$y$的存在性已知,所以必然会停机接受;否则对于无法接受的字符串必然是停机的结局。
故$L$可识别。
左推右:有可识别性,则存在图灵机M:
\[L=\{x\mid\exist y=\langle C_0,...C_m\rangle,为M在x上的接受计算\}\]那么根据已知的$y$,就可以构造可判定语言C,本质上就是一个字符串比较:
\[C=\{\langle x,y\rangle \mid y是M在x上的接受计算\}\]—-从而证毕—-
由上定理知:
\[\bar L=\{x\mid \forall y, <x,y>\in\bar C\}\]从而可以给出L补图灵可识别的等价条件:
\[L=\{x\mid \forall y, <x,y>\in C\}\]再考虑TM空性问题(Emptyness)
- 我们断言:$E_{TM}={
\mid L(M)=\emptyset\}$是补图灵可识别的。
对于$\bar E_{TM}$,它实质上是TM满性问题
只需要考虑任何一个输入即可:
$E_{TM}={\langle M\rangle \mid \forall x,y,y不是M在x上的接受计算}$
证毕。
和之前的构造相同,我们也需要考虑不停机的问题。
可以用楔形过程;或者规定最大运行n步。
接下来考虑TM满性问题:
\[All=\{\langle M\rangle\mid L(M)=\Sigma^*\}=\{\langle M\rangle\mid \forall x,\exist y,y是M在x上的接受计算\}\]考虑到数理逻辑中的一个定义和此处量词的关系:
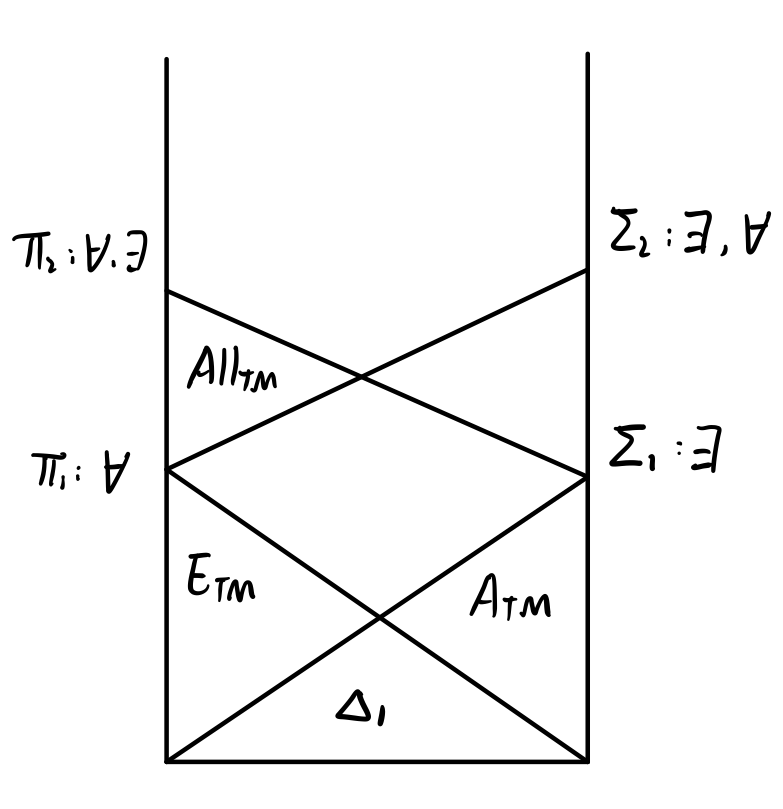
- $\Pi_n$和$\Sigma_n$前束范式:
- 设$n>0$,若前束范式是由全称量词开始,从左至右改变$n-1$次词性,称为$\Pi_n$型前束范式;
- 若是由特称量词开始的,从左至右改变$n-1$次词性,称为$\Sigma_n$型前束范式;
为什么只论改变呢?因为中间不变的都可以用多元组变成一个元素。。。
特别地,称可判定问题为$\Delta_1$.
3 归约-reduction
归约的目的有两个,一个是转换;一个是简化。首先先介绍转换。
3.1 引入
所谓问题$A$归约到问题$B$,其核心就是我们可以用问题$B$的答案来解决$A$。这也就是问题$A$不比问题$B$难的由来。
当我们找到问题$B$的一个解时,就可以找到$A$的一个解。
通常我们用停机问题$HALT_{TM}$来介绍一个简单的思维,也就是反证法。
证明:
假设$HALT_{TM}$可以判定,则考虑$A_{TM}$的解。
构造解图灵机A:对于输入“$\langle M,w\rangle$”
- 模拟H的运行,如果拒绝就拒绝;
- 如果接受,那么就在$w$上运行$M$;
- 接受则接受,拒绝则拒绝。
从而就构造了一个对$A_{TM}$的解,而事实上这是不可能的。
归约的核心是,从B的一个解得到了A的一个解。之后在多一归约中,我们会介绍一种方法。
这里我们必须再给出一个例题,它是理解多一归约的敲门砖。
- 定理:$E_{TM}$是不可判定的。
证明:
仍然考虑$A_{TM}$的归约。我们仍然使用反证法。
不过我们需要改造一下,对于$\langle M,w\rangle\in A_{TM}$,构造
$M_1$:对于输入$x$,有
- 如果$x\neq w$,就拒绝;
- 反之则运行M,如果接受就接受。
如果$E_{TM}$是可判定的,考虑其判定机E,来构造$A_{TM}$的解:
$A$:对于输入$\langle M,w\rangle$
- 构造$M_1$,并用E来判断它
- 如果接受,就拒绝;如果拒绝,则接受。
如果E接受,就说明$M_1$接受的语言为空,说明$M$不会接受任何串;反之,其接受串$w$
以上就完成了对它的证明。
3.2 定义-映射可归约性
- 定义3.1.1:函数$f:\Sigma^\to\Sigma^$是一个可计算函数。指存在一个图灵机$M$,使得对于每个输入$w$,$M$都停机,且只有$f(w)$留在带子上。
接下来,我们就可以给映射可归约性下一个形式化定义。
- 定义3.1.2:对语言来说,$A$可归约到$B$,记作$A\le_m B,via\ f$。其中$f$为可计算函数。
- 对每个$w\in A$,均有$f(w)\in B$,反过来依然。
具体可见下图:
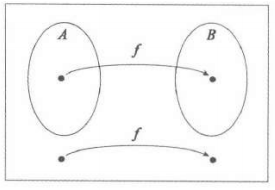
对于这样一个归约,我们称:
- A不比B难
- B不比A容易
据此有定理:
- 定理:如果$A\le_m B,via\ f$,则:
- B可判定,则A可判定;
- A不可判定,则B不可判定。
借用可计算函数定义中的图灵机即可证明。
例题1:
- $E_{TM}$不可判定。
考虑$A_{TM}\le_m \bar E_{TM}$,则$f:\langle M,x\rangle\mapsto\langle M’\rangle=f(\langle M,x\rangle)$,即:
$M$接受$x\iff L(M’)\neq \emptyset$
- 考虑$M’$的构造(实质上就是考虑$f$的具体构造)
$TM\ M’$:对于输入$y$有
- 模拟$M$在$x$上的运行;
- 若$M$接受,则接受;其拒绝则拒绝。
- $f$可计算性证明
这一步是为了判断$f$的定义是否合理,也就是能不能处处停机。从1中构造方式来看,这种构造必然是可以的。
- 归约正确性证明
对于$\langle M,x\rangle\in A_{TM}$
当且仅当$M$接受$x$,此时$L(M’)=\Sigma^*$,则$M’\in \bar E_{TM}$
而我们知道,前者不可判定,故后者不比前者简单,所以必然不可判定。
大致的证明步骤均同上。
至于归约的方向,我们可以根据下图来判断。

等高的结果是不能互相归约的,只能从下到上归约。
类似于前面的反证法证明,我们试图说明多一归约的核心。
例题2:$ALL_{TM}$不可计算。
类似地,按照$A_{TM}\le_m ALL_{TM}$构造$f:\langle M\rangle\mapsto\langle M’\rangle$
事实上,我们还可以得到:
- $E_{TM}\le_m ALL_{TM}$
- $\bar E_{TM}\le_m ALL_{TM}$
例题3:$REG_{TM}={\langle M\rangle\mid L(M)是否属于正则语言}$不可计算。
构造$M’$:
- 对于输入$x$,模拟$M$;
- 若接受,则考察y是否是$0^n1^n$,是则接受,否则拒绝;否则拒绝。
3.2 映射可归约的性质
有传递性和封闭性
- $A_{TM}$是$\Sigma_1$完备的。即对$\forall L={x\mid \exist y, \langle x,y\rangle \in C}$。$L\le_m A_{TM}$
证明:
考虑$x\mapsto \langle M,x\rangle$,此处$x$保持同一性。
只需要枚举$y$即可构造。
- 定理3.2.1(Rice 定理):
- 定义指标集$I={\langle M\rangle\mid …}$;
- 我们断言,任何非平凡(空、满)的指标集都是不可判定的。(对图灵机的非平凡性质不可判定)
证明:
考虑一图灵机$M_0$,满足$L(M_0)=\emptyset$
检查第一种情况:$\langle M_0\rangle\in I$
由$I$的不平凡性,必然有$M_1\notin I$。下证$A_{TM}\le_m \bar I$
流程类似:$M_0$跑$x$,能过就用$M_1$跑$y$,接受就接受,否则都不接受。
所以$L(M’)$:
- 当$M$接受$x$,则$L(M’)=L(M_1)\notin I,\in \bar I$;
- 反之,则$L(M’)=L(M_0)\in I,\notin \bar I$。
证毕。另一考察类似。
3.3 利用计算历史归约
核心就是把输入解码成计算历史。由于一个图灵机的接受计算或者拒绝计算都是有穷的,所以必然可以判定。这种图灵机归约的不停机情况在无穷枚举序列上。
用接受计算历史归约,就是把输入解码成历史,然后再判定。即满足:
设解码得到的格局序列为$c_0,c_1,…,c_m$,则
- $c_0$为初始格局;
- $c_i\to c_{i+1}$符合图灵机M的转移函数;
- $c_m$为接受格局。
这样,我们给出图灵机M’的精确描述:
M’ = “对于输入y,
- 解码得到$y=\langle c_0,c_1,…,c_m\rangle$,
- 检查$c_0$是否为初始格局,若不是则接受,
- 依次检查$c_i\to c_{i+1}$是否满足M的转移函数$\delta$,若至少有一个不满足则接受,
- 检查$c_m$是否为接受格局,若不是则接受。”
有趣的是,这件事情,LBA也可以做,PDA也可以做,但PDA只能做一部分,它只能判断错误的情况,这是由其不确定性保证的。
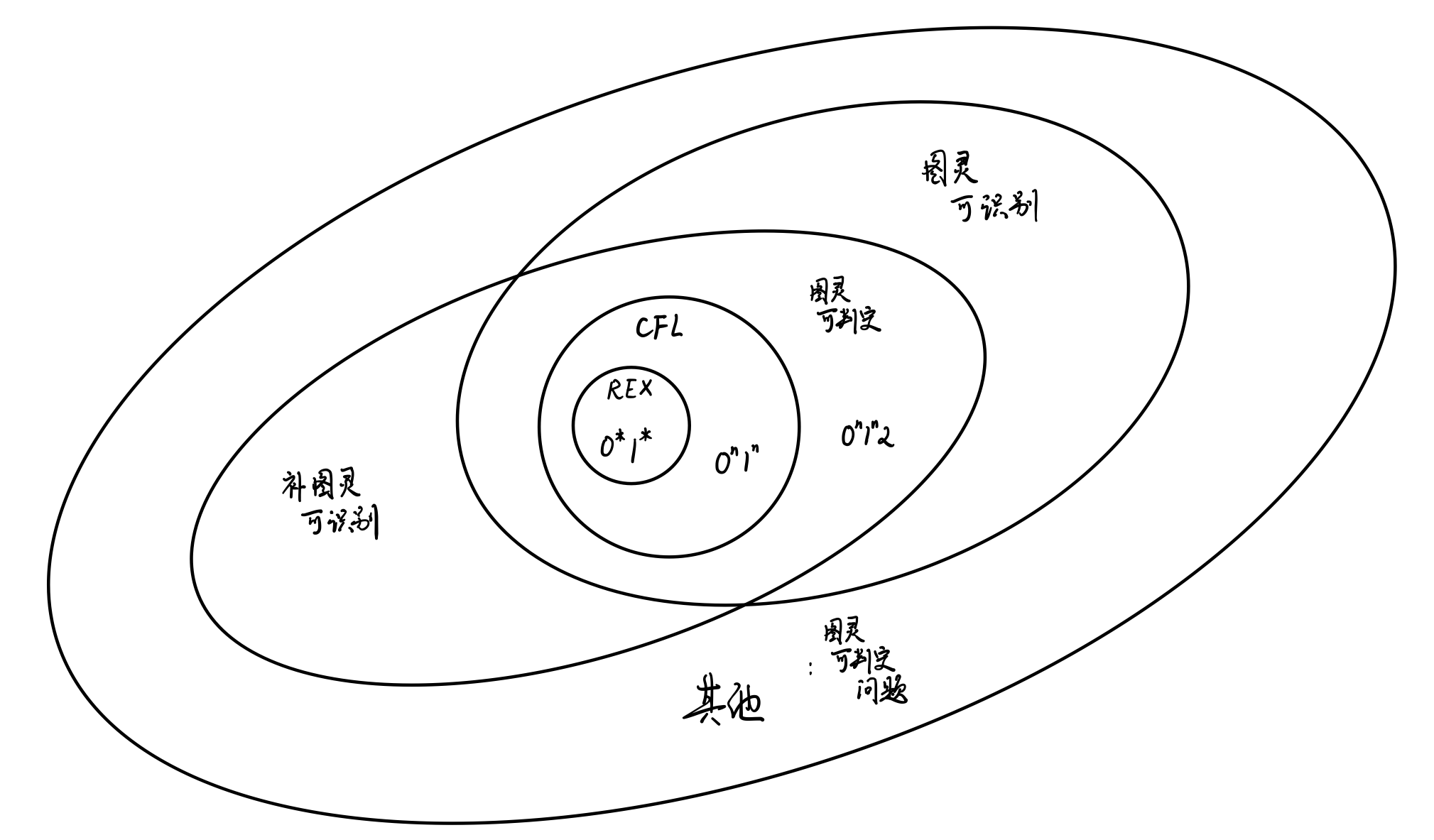
我们用乔姆斯基谱系来为之前学过的(广义的)自动机和语言作分类:
| 乔姆斯基谱系 | 语言类 | 自动机 |
|---|---|---|
| 3型文法 | 正则语言 | DFA,NFA,REX |
| 2型文法 | 上下文无关语言 | PDA,CFG |
| 1型文法 | 上下文有关语言 | LBA,CSG |
| 0型文法 | 图灵可识别语言 | TM |
线性界限自动机(LBA, Linear Boundary Automata):只能在输入区工作的图灵机。即纸带上输入字符串所占据的空间就是读写头移动的空间,不允许读写头离开包含输入的带子区域。
另一方面,我们可以肯定的是,LBA是可以判断不停机的情况。因为固定长度的输入,必然会导致图灵机格局的有限,所以可以通过枚举所有格局数量来判断是否进入循环。
对每种谱系,我们均关心四个问题:接受性($A_M$)、满性($All_M$)、空性($E_M$)、等价性问题($EQ_M$)(这里M可以为自动机DFA,NFA,REX,…,TM之一)。这四种问题的定义跟图灵机中的定义基本一致。
若以√表示问题可判定,以×表示问题不可判定,则有下表:
| 乔姆斯基谱系 | 语言类 | 自动机 | 接受性 | 空性 | 满性 | 等价性 |
|---|---|---|---|---|---|---|
| 3型文法 | 正则语言 | DFA,NFA,REX | √ | √ | √ | √ |
| 2型文法 | 上下文无关语言 | PDA,CFG | √ | √ | × | × |
| 1型文法 | 上下文有关语言 | LBA,CSG | √ | × | × | × |
| 0型文法 | 图灵可识别语言 | TM | × | × | × | × |
4 递归定理
递归定理最初是由递归函数论发展,由递归函数给出了关于计算性的描述,后来证明和图灵机等价,所以递归定理也有相应的图灵机形式,显得更加直观。
4.1 递归定理的四种等价形式
Kleene第二递归定理
\[\forall computable\ t: \Sigma^ * \times \Sigma^ * \to \Sigma^ * via\ \ TM\ \ T, \\\exists TM\ R, \quad s.t.\ \ \forall y\in \Sigma^ * , \quad t(\langle R\rangle , y)=R(y)\]此处的可计算函数t与之前定义稍有不同,对于未定义的输入,可以选择停机或者不停机。我们采取不停机。
不动点定理
\[\forall computable\ t: \Sigma ^ * \to \Sigma ^ *,\quad\\ \exists TM\ F,\quad s.t.\ \ F与t(\langle F\rangle )对应的图灵机等价\]即$F$与$t(\langle F\rangle )$对应的图灵机接受相同的语言。
图灵机自引用
定义图灵机时,允许它引用自己的编码,即如下形式的描述是合法的:
图灵机M = “…………$\langle M\rangle$…………”
这一点对于日常生活所用的语言来说十分平凡,但是在逻辑上,自引用是一个十分强的约定。
图灵机自复制
\[\exists TM\ \ \ SELF, \forall x\in \Sigma^*, SELF(x)=\langle SELF\rangle\]4.2 证明
$①\Rightarrow ②$
已知可计算函数$t: \Sigma^ * \to \Sigma^ *$,构造①中的可计算函数t所对应的图灵机T:
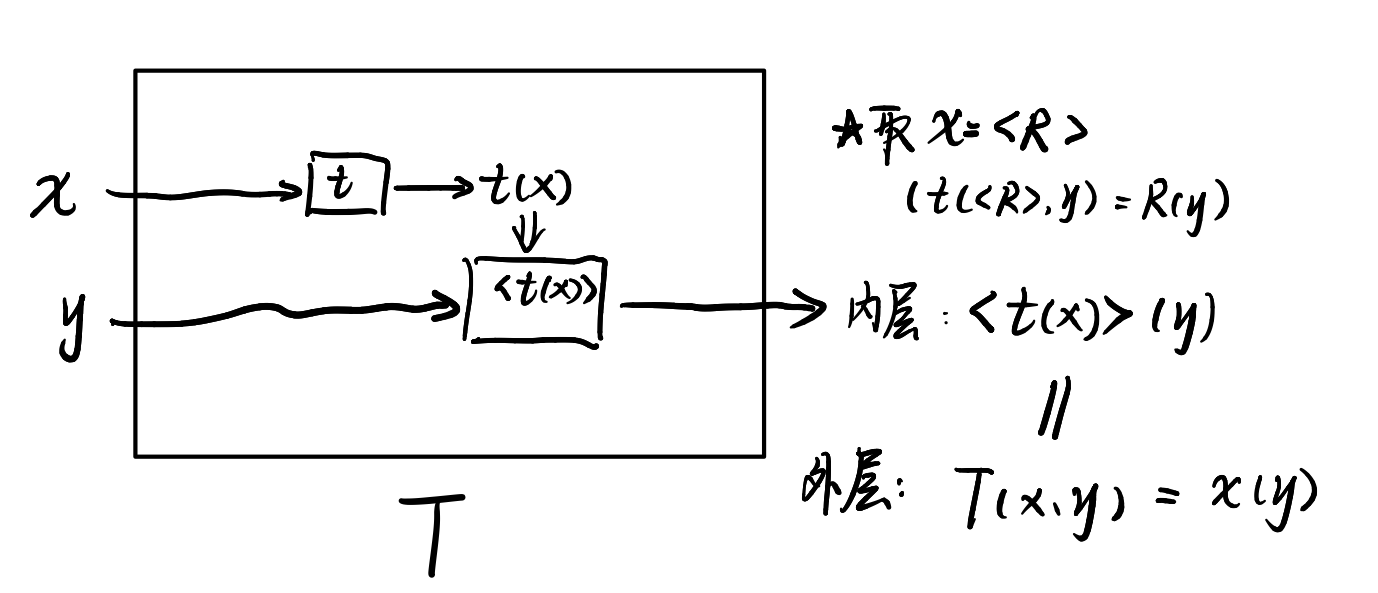
由第二递归定理,存在图灵机F,满足$T(\langle F\rangle,y)=F(y)$。
由T的构造,$T(\langle F\rangle,y)=t(\langle F\rangle )(y)$。
因此$t(\langle F\rangle )(y)=F(y)$,即$t(\langle F\rangle )=F$,这就是②的结论。
该证明的核心是利用递归定理中的$t(\langle R\rang,y)=R(y)$
$②\Rightarrow ③$
任给一个可计算函数$t:\Sigma^ * \to\Sigma^ * $,由②,存在一台图灵机M,满足$M$与$t(\langle M\rangle)$对应的图灵机等价。
因$\langle M\rangle$作为自变量,故描述$t(\langle M\rangle)$对应的图灵机时会用到$\langle M\rangle$,即$t(\langle M\rangle)$对应的图灵机的描述具有如下形式:
$t(\langle M\rangle)$ = “…………$\langle M\rangle$…………”
由$M$与$t(\langle M\rangle)$等价,亦可以将M描述为
$M$ = “…………$\langle M\rangle$…………”
本质上利用不动点的不变性,实际上是一个例化过程。
$③\Rightarrow ④$
定义图灵机SELF:
SELF = “对于输入x,删除x,由定理③得到$\langle SELF\rangle$,打印出$\langle SELF\rangle$并停机。”
$④\Rightarrow ①$
核心在于构造图灵机R。令$R=ABT,A:=P_{\langle BT\rangle}$,其中T为①中已知的二输入图灵机T,$B$为④的证明过程中所构造的图灵机。与④略有不同,为了使这台图灵机能够接受纸带上的输入w,我们重新设计$P_s$,使得$P_s$先打印输入内容,再打印w,即$P_s(w)=ws$。
这样,$R(y)=(P_{\langle BT\rangle}BT)(y)=(BT)(y\langle BT\rangle)\stackrel{!}{=}T(\langle P_{\langle BT\rangle }BT\rangle,y)=T(\langle R\rangle, y)$
最后一步:证明$④$
定义图灵机$P_w$:
$P_w$ = “对于输入x,删除x,打印w并停机。”
定义图灵机Q:
Q = “对于输入w,得到图灵机$P_w$,打印$\langle P_w\rangle$并停机。”
定义图灵机B:
B = “对于输入$\langle M\rangle$,用Q计算出$\langle P_{\langle M\rangle}\rangle$,打印$\langle P_{\langle M\rangle}M\rangle$并停机。”
记图灵机$A=P_{\langle B\rangle}$。
我们断言:$\langle SELF\rangle=\langle AB\rangle$
取$A=P_{\langle B\rangle}$,故$y=\langle B\rangle$,故输出$B(y)=B(\langle B\rangle )=\langle P_{\langle B\rangle }B\rangle=\langle AB\rangle=\langle SELF\rangle$。
4.3 应用
4.3.1 $A_{TM}$不可计算性的递归证明
例题1 证明
\[A_{TM}=\left\{\langle M,x\rangle\mid M接受x\right\}\]不可判定。
证明:反证。假设存在图灵机H判定$A_{TM}$,构造图灵机D:
D = “对于输入x,
将$\langle D,x\rangle$送入H,若H接受则拒绝,反之则接受。”
那么这个机器本身就矛盾了。因为D的行为是由H定义的,反过来不是找死吗? 笑~
4.3.2 极小图灵机问题
例2 证明
\[MIN_{TM}=\left\{\langle M\rangle\mid \forall M', \left|\langle M'\rangle\right|<\left|\langle M\rangle\right|\Rightarrow L(M')\neq L(M)\right\}\]不可判定。
- 更直白的说,在同等能力下,没有人比它更懂缩短编码。
证明:我们首先证明$MIN_{TM}$不是图灵可识别的。为此,我们给出图灵可识别的另一个等价定义:图灵可枚举。
一个语言$L$是图灵可枚举的,如果存在一个图灵机T,它不接受输入(或者说输入为空),而能够打印该语言中的所有串。我们称这样的图灵机为枚举机。
证明L是图灵可枚举的$\Leftrightarrow$L是图灵可识别的:
$\Rightarrow$:L是图灵可枚举的,要证明它是图灵可识别的,只要考察任何一个输入$x\in \Sigma^ * $。运行枚举机,枚举L中的串,如果$x\in L$,枚举机必定能在有限长时间内枚举到某个串$w_i=x$,这时停机接受。否则,如果L有穷,枚举机会停机拒绝,不然枚举机不会停机。这与图灵可识别的定义一致。
$\Leftarrow$:L是图灵可识别的,假设图灵机T识别L,运行T,按楔形过程枚举$\Sigma ^ * $中的全部串,如果某个串被接受,就将它打印出来。这就实现了枚举L中的全部串。
我们下面证明这样一个结论:$MIN_{TM}$中不含图灵可识别的无穷子集。即对于$MIN_{TM}$的任何一个子集,只要这个子集中有无穷多个元素,它就不是图灵可识别的。
反证。由图灵可识别与图灵可枚举的等价性,如果某个无穷子集(设为$A$)是图灵可识别的,就一定存在一台枚举机E,它能枚举$A$中的所有元素。构造下列图灵机C:
C = “对于输入w,
- 由递归定理得到它自己的描述$\langle C\rangle$。
- 运行枚举机E,因A中有无穷个元素,故必定存在某个图灵机D,满足$\mid\langle D\rangle\mid>\mid\langle C\rangle\mid$。
- 在D上运行w。”
按如上定义,D可以完全定义一台比它更短的图灵机行为,矛盾!因此A不是图灵可识别的。同样地,因$MIN_{TM}\subseteq MIN_{TM}$,这就有$MIN_{TM}$也不是图灵可识别的。证毕。
4.3.3 图灵可识别集与可判定子集
定理 任一无穷图灵可识别语言都有无穷可判定子集。
证明:要证明这一定理,首先要证明一个引理:
引理 L可判定$\Leftrightarrow$L递增图灵可枚举。
递增图灵可枚举是说枚举机可以按照递增序(由短到长)枚举L中的所有串。证明这条引理:$\Rightarrow$:按照由短到长的顺序逐个判定所有的串即可;$\Leftarrow$:因为枚举机按照递增序枚举,对于给定的串,如果能枚举到这个串,就接受,否则如果递增地枚举到了比它还长的串,就拒绝。
这样这条定理就有了等价表述:任一无穷图灵可判定语言都有无穷递增图灵可枚举的子集。
不妨设L是一个无穷图灵可枚举语言,枚举它的元素$w_1,w_2,…$,设它们的长度分别为$l_1,l_2,…$。我们的目的是找到L的一个无穷递增图灵可枚举的子集SL,它的元素为$w_{s_1},w_{s_2},…$,且满足$l_{s_1}\leq l_{s_2}\leq …$,其中指标集
\[S=\left\{s_1,s_2,...\right\}\subseteq \mathbb{N}\]换句话说,我们要证明,任一无穷非负整数序列必有无穷递增子序列。
5 图灵归约
5.1 定义
回顾一下多一归约的定义:
- $A\le_m B \ via\ f,s.t. x\in A\iff f(x)\in B\quad(computable\ f)$
我们主要依据可计算函数,这一点要求很强,但带来的结果却不够强。
多一约束性很强,但能力不够强。这里的能力指:许多问题没办法判断强弱。
所以接下来我们介绍一个要求低,但结果强的归约—图灵归约,又写作T-归约。
- $A\le_T B\ via\ M^B, A=L(M^B)$,其中这个怪异的定义为谕示图灵机(Oracle TM or OTM for short)
- 谕示图灵机:它比正常图灵机多了一条带用于查询,其上可以写上一个字符串,进入状态$q_{query}$,并增加$q_{yes},q_{no}$两个状态用来判断写上的串$y$是否属于$L(B)$
比如说,我们使用的互联网。又或者我们在写C程序时,不想做大数运算,就交给Python去做,然后得到数据后打表存在C语言中,这也是一种查询的办法。
m-归约对于补运算十分敏感,但对于问题难易来说,补运算往往没那么重要。而图灵归约便避开了这个弱点。
5.2 性质
5.2.1 $\le_m$弱于$\le_T$
这一点在定义中就可以看出来。由于多一归约的可计算函数可以由图灵归约中的图灵机定义;
而图灵归约中的谕示图灵机在多一归约中并没有直接体现。
比如:$A_{TM}\le_T \overline{A_{TM}},but\ A_{TM}\nleq_m \overline{A_{TM}}$
前者只需要询问输入是否在$A_{TM}$中,并对结果取反即可。
这种询问都是假定在后一问题可解的情况下完成的。这样的归约更贴近于我们的认知。
5.2.2 传递性显然
5.2.3 封闭性
| 可判定问题 | 图灵可识别问题 | 补图灵可识别问题 | |
|---|---|---|---|
| $\le_m$ | $\surd$ | $\surd$ | $\surd$ |
| $\le_T$ | $\surd$ | X | X |
这里我们可以引入相对化计算:
- $M^B$:相对于B问题可判定,属于带谕示的计算。
由此可以:
\[\Sigma_2 = \Sigma_1^{A_{TM}}\\ \Pi_2 = \Pi_1^{A_{TM}} \\ \Delta_1 = \Sigma_1\cap\Pi_1\\ similarly:\Delta_2 = \Sigma_2\cap\Pi_2\]- 定理:$\Sigma_2 = \Sigma_1^{A_{TM}} = \Sigma_1^{\Sigma_1}$
证明:我们只证明前一个等号,后一个等号由于$A_{TM}$是$\Sigma_1$完全的。
$①\Sigma_2\subseteq \Sigma_1^{A_{TM}}:$
\[\forall L\in\Sigma_2\Longrightarrow L=\{\langle x\rangle\mid \exist y_1,\forall y_2,\langle x,y_1,y_2\rangle\in C\}\] \[define:L_1=\{\langle x,y_1\rangle\mid \forall y_2,\langle x,y_1,y_2\rangle\in C\}\in\Pi_1\Longrightarrow\overline{L_1}=L(M_1)\] \[Then:\overline{L_1}\le_m A_{TM}\ via\ f:x\mapsto \langle M_1,x\rangle=f(x)\]对L,由此定义TM $M^{A_{TM}}=$”对于输入$x$”
- 枚举$y_1$,查询$\langle x,y_1\rangle$是否属于$\bar L_1$
- 若结果为否,则接受。
本质上就是用量词描述语言,然后将任意量词交给OTM。即可。
$②\Sigma_1^{A_{TM}}\subseteq \Sigma_2:$
\[\forall L\in \Sigma_1^{A_{TM}}\Longrightarrow L=L(M^{A_{TM}})\]对于输入$x$,$M^{A_{TM}}$将其计算结果分成两类进行询问,一类是给出yes的$y_i$;一类是给出no的$n_j$。
对于前者,我们必然存在接受计算串序列;对于后者对任意序列串都不接受,如此就能定义出$\Sigma_2$。由此证毕。
5.3 应用
- 语言类的刻画
- 相对化计算
- 搜索规约的判定
- 比如对SAT问题的递归搜索判断。