1 复杂性度量
在可计算性中,我们区分无限与有限;
而到了复杂性理论,我们在有限的基础上,继续细分,划分为:
- 多项式时间的有效计算
- 指数时间的无效计算
1.1 大O记法
为什么称多项式时间计算十分有效呢?
一是因为$\mathbb{R}[X]$是一个环,而且对递归运算也是封闭的。
二则是这是因为多项式时间下,求解开销随问题规模增长合适。
在这里没必要纠结什么叫合适。比如对$n^2$,改进速度到原来的两倍,问题规模就可以稳定扩大$\sqrt{2}$,而指数$2^n$仅仅只能+1.
以上,我们可以定义:
- $t_M(x):=$M在x上的运算步数;
- $S_M(x):=$M在x上运行所用空格数。
前者是本节的重点,时间复杂性;而后者是下一节的重点,空间复杂性。
此外,在算法分析中,我们考虑最坏情况;而在密码学中,我们考虑平均情况。这是因为密码学需要保证大部分计算都是难的。
\(t_M(n):=\max_{x\in\Sigma^n,|x|=n}{t_M(x)}\) \(t_M(n):=avg_{x\in\Sigma^n,x\sim D}{t_M(x)}\)
此外还有平滑分析,平锥分析等。
由线性加速定理:
- $\forall TM\ M_1, t(n), \exist c>0,s.t. \exist TM\ M_2\ has\ t(n)/c$,且$L(M_1)=L(M_2)$
只需要将c个状态合并成一个即可。
由此可以用$O,o$渐进分析。
由此做一个简单的分类:
| name | t | one by one | parallel |
|---|---|---|---|
| log | $\log n$ | $\surd$ | $\surd$ |
| poly-log | $\log^k n$ | $\surd$ | $\surd$ |
| sub-linear | $n^{1-\epsilon}$ | $\surd$ | $\surd$ |
| linear | $n$ | $\surd$ | |
| poly | $n^k$ | $\surd$ | |
| super-poly | $n^{\log^k n}$ | $\surd$ | |
| sub-exp | $\bigcap_{\epsilon>0}2^{n^\epsilon}$ | $\surd$ | |
| exp | $2^{n^k}$ | ||
| double-exp | … |
1.2 常用的时间复杂性类
- $P := \bigcup_{k>0}TIME(n^k)$
- $NP := \bigcup_{k>0}UTIME(n^k)$
- $CONP := \overline{NP}$
- $EXP := \bigcup_{k>0}TIME(2^{n^k})$
- $NEXP := \bigcup_{k>0}NTIME(2^{n^k})$
事实上,我们对它们的认知十分简单。我们尚不能确定很多事情:
- ? NEXP=CONEXP
- ? NP =CONP
- ? NP$\cap$CONP = P
- ? P = NP
- $P\neq EXP$
已知:
- $NP\subseteq EXP$
1.3 模型间的复杂性关系
- 定理:$t(n)\ge n$,则每一个$t(n)$时间的多带图灵机都和某一个$O(t^2(n))$时间的单带图灵机等价。
证明:模拟$k$带图灵机行为,需要两步。第一步扫描带子,获取转移的信息;第二步遍历,完成自己的动作。现分析其需时。
由于在$t(n)$步时,哪怕带头一直向右移动,也不过是$k\times t(n)$个格子。如果一直模拟到第$t(n)$步。需要求和,所以大致是$O(t^2(n))$步。
最后考虑初始化,也就是单带图灵机需要让带子形成合适的格式。这需要$O(n)$步。
综上可知证毕。
从该定理可知,多带图灵机之间差别“不明显”。P还是P问题,NP还是NP问题。
进一步考虑非确定性。情况有所变化。
- 定理:$t(n)\ge n$,则每一个$t(n)$时间的非确定图灵机都和某一个$2^{O(t(n))}$时间的单带图灵机等价。
证明:非确定会生成一个计算树,利用BFS加上最大度数b,即可证毕。
考虑到需要输入、模拟、地址选择三条带子。但是用上一个定理取平方在指数上也是常数级,自动并入。
3 P与NP问题
3.1 P类问题举例
- 例题1:$PATH\in P$
BFS即可。可以在$O(\mid V\mid )$内实现。
- 例题2:$RELPRIME\in P$
欧几里得算法即可。
- 例题3:每一个上下文无关语言都是P的成员
如果利用之前的CNF操作,枚举2n-1步生成n长度的串$w$。如果生成式合适,可以达到指数倍数的选择。比如每一步生成都有k个选择的话。
这里使用一种动态规划算法。利用表格对串进行从小到大的讨论。

3.2 NP类问题举例
NP问题有三种定义:
- 确定型图灵机非多项式时间可计算
- 非确定型图灵机多项式时间可计算
- 确定型图灵机多项式时间可验证
就验证而言,定义:
- 语言$A$的验证机是一个算法$V$:
验证机利用额外的信息来验证字符串$c$是$A$的成员。该信息成为$A$的成员资格证书后者证明。
比如哈密顿路径直接给出路径;合数问题直接给出因子。
- 例题4: $CLIQUE\in NP$
证明:
验证机V:对于输入$\langle \langle G,k\rangle,c \rangle$
- 检查c的顶点是否在G内;
- 检查c的边是否都在G内;
- 若都通过则接受,否则拒绝。
判定机:对于输入$\langle G,k\rangle$
- 非确定地选择k元素顶点子集
- 检查
- 若是则接受。■
- 例题5:$SUBSET-SUM\in NP$
证明:
验证机V:对于输入$\langle \langle S,t\rangle,c \rangle$
- 检查c的和,与t比较
- 检查c的元素是否都在S内;
- 若都通过则接受,否则拒绝。
判定机:对于输入$\langle S,t\rangle$
- 非确定地选择S子集c
- 检查
- 若是则接受。■
注意到这些集合的补集不是很明显地属于NP。验证某种事物不存在貌似比证明存在要更为困难。
4 NP完全类问题
在P和NP问题上的一个重大进展是库克和列文完成的。他们发现NP中某些问题的复杂程度与某个类的复杂程度相关。这些问题称为NP完全的。
历史上给出的一个NP完全问题称为可满足性问题SAT。
\[SAT:=\{\langle\phi\rangle\mid \phi\ is\ satisfiable\}\]4.1 多项式时间可归约性
\[A \le_m^p B\ via\ f\iff (f\in FP,\ and \forall x\in A \iff f(x)\in B)\]性质:
- 传递性
- 封闭性,P,NP,CONP
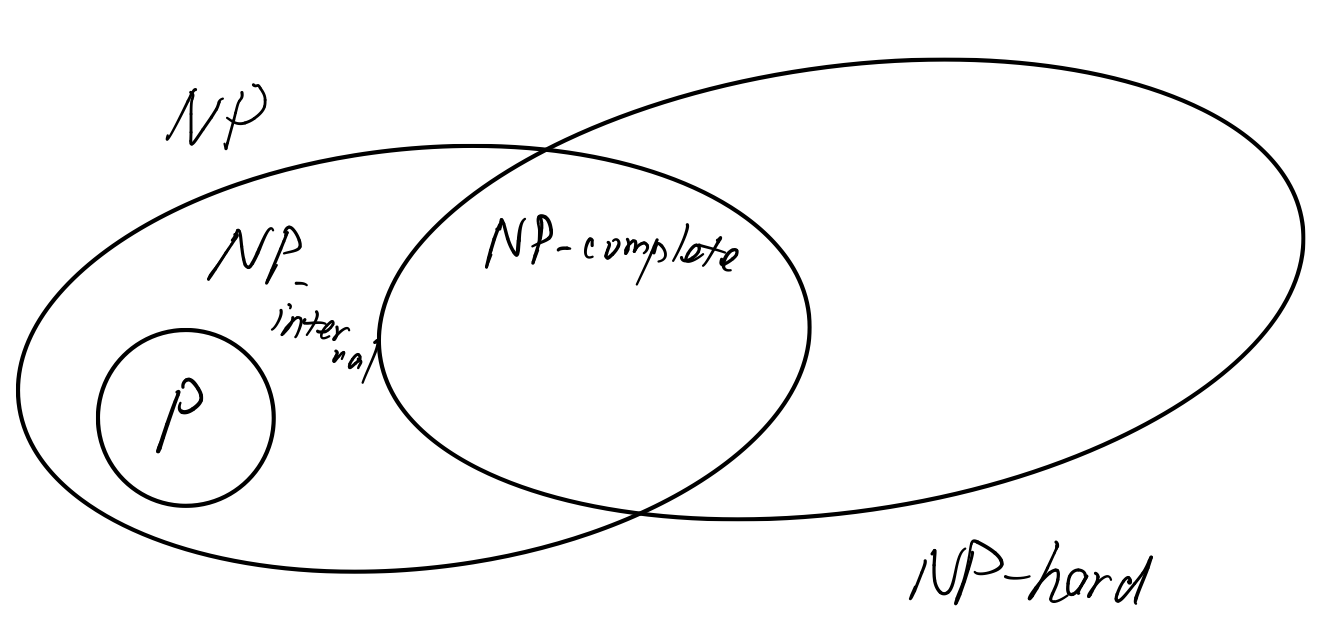
4.2 NP类的结构
- NP-hard:$\forall L\in NP, L\le_m^p A$,则A是NP难
- NP-complete:$A\in NP$,A是NP-hard。
注意,NP难和NP问题不一定是一样的。NP问题需要在NP内解决,而NP难问题未必能在NP内解决。比如阶乘时间内才能解决。
- 定理:$A$是NP难的,且$A\in P$,则$P=NP$
4.3 库克-列文定理
- 首先证明SAT问题是NP问题
利用NTM非确定地枚举一个赋值验证即可。
- 再证明其为NP难的
由于需要对任何一个属于NP的语言作多项式时间归约,所以为了一般性,只能采用计算历史归约。
考虑$\forall A\in NP\ with\ decider\ TM\ N$
在输入$w$上,定义画面:
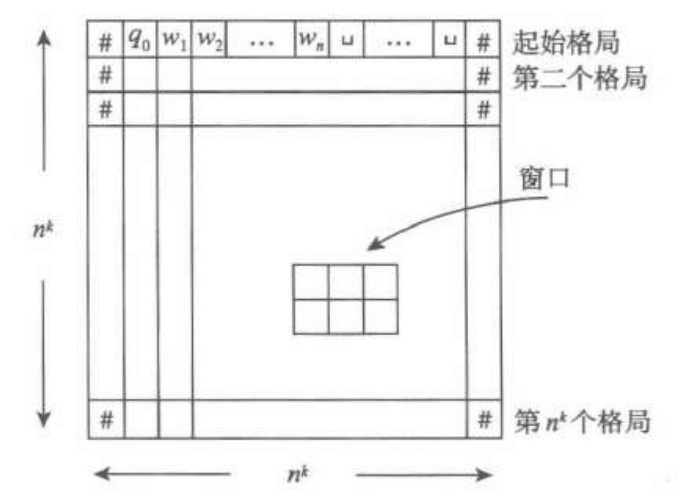
所以判定是否存在$N$在$w$上的接受画面,与是否接受等价。
现在设计一个$\phi$,使得变量的一个满足赋值确定对应一个接受画面。
\[\phi = \phi_{cell} \wedge \phi_{start} \wedge \phi_{move} \wedge \phi_{accept}\]规定:
\[x_{i,j,s}\ means\ put\ 's'\ in\ Cell[i,j]\]为保证每个Cell只有一个符号,则:
\[\phi_{cell}=\wedge_{i\le i,j\le n^k}[(\vee_{s\in C}x_{i,j,s})\vee(\wedge_{s,t\in C,s\neq t}(\overline{x_{i,j,s}}\vee\overline{x_{i,j,t}}))]\]第一部分保证必然有一个符号在格子内,第二部分保证了只有一个符号在其中。
\[\phi_{start} = x_{1,1,\#}\wedge...\wedge x_{1,n^k,\#}\]就是确保第一行是这个样子,是初始格局。
\[\phi_{accept}=\vee_{1\le i,j\le n^k}x_{i,j,q_{accept}}\]保证最后一行存在接收状态。
最后比较麻烦的是保证转移是合理的,也就是move的任务。
我们保证一个$2\times 3$的窗口是合法的。也就是:
\[\phi_{move}=\wedge_{1\le i<n^k,1<j<n^k}(Cell[i,j]\ is\ reasonable)\]我们取$a,b,c,d,e,f$作为合法窗口的符号,然后只需要确保每一个窗口内都能和某一种合法窗口对应,也就是:
\[\vee_{a,...,f}(.\wedge...)\]最后,我们分析归约的复杂性。证明它的确能在多项式时间内完成。
考察$\phi$的大小:
- 变量数目,$\mid C\mid$只与N有关,故变量总数为$O(n^{2k})$
- cell段长度固定,为$O(n^{2k})$
- move,start,accept固定,均不超过$O(n^{2k})$
- 公式的生成形式上高度一致,只有下标的变化,故完全可以构造。■
4.4 3SAT问题
显然其为NP问题,接下来可以直接采用变换,将上述定理的证明稍加修改即可。
首先是把move转化成CNF形式,由合取析取性质可知能成。
然后是变化,可以加入多个变元来选择,类似于选择器一样:
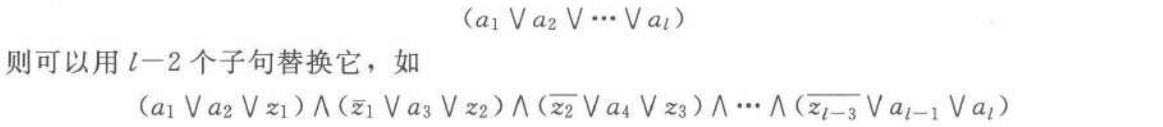
5 更多NP完全问题
5.1 定点覆盖问题
\[VERTEX-COVER:=\{\langle G,k\rangle\mid G是具有k个顶点的顶点覆盖无向图\}\]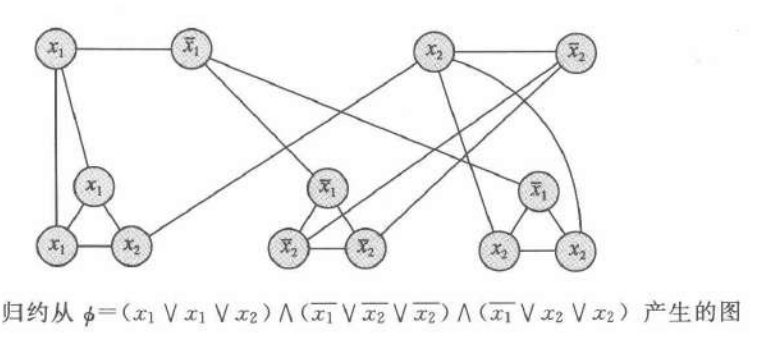
即可。
5.2 HAMPATH
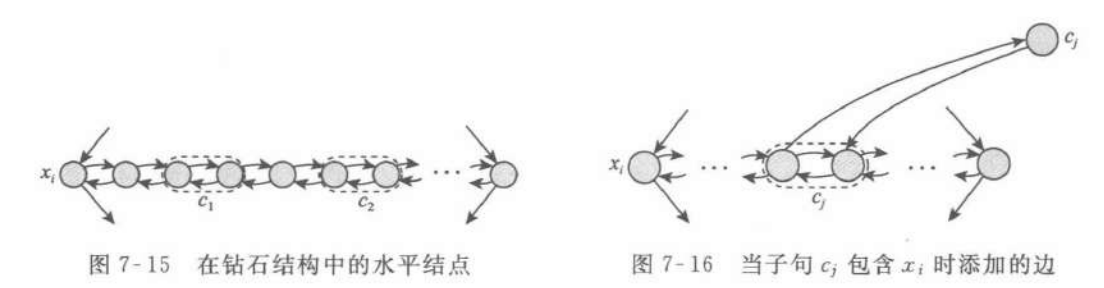
5.3 UHAMPATH
将顶点拆分成:
\[u_{in},u_{middle},u_{out}\]则方向化作了点的连接,over。
5.4 SUBSET-SUM
\[SUBSET-SUM:=\{\langle S,t\rangle\}\]
即可。