这篇博文记载脑机接口导论书籍的基础部分, 主要为1-5章. 在阅读几篇论文之后, 发现基础缺失过多, 于是特来弥补一下.
chapter-1: 引言
BCI的实现通常设计下述一个或多个处理步骤:
- 脑信号的记录
- 信号处理
- 模式识别或机器学习(构建脑信号的解码器)
- 感知反馈
- 刺激信号处理
- 脑刺激
BCI至少需要四个方面的知识: 基础神经科学, 大脑信号记录和刺激计数, 基本的信号处理技术, 机器学习技术. 这也就构成了之后四个章节的内容.
chapter-2: 神经科学基础
人脑独特的信息处理能力得益于其大规模的并行和分布式计算方法. 另外, 神经元之间的连接是可塑的, 这使得大脑的神经网络能够适应新的环境变化.
传统计算机是基于冯诺依曼结构的, 由独立的中央处理器单元和存储单元组成, 元件之间保持固定的连接方式, 多为串行结构.
2.1: 神经元
神经元是一种细胞, 通常被认为是神经系统最基本的计算单元.
神经元存在于水介质中, 细胞外的$Na^+$浓度明显大于内部的, 而内部的$K^+$则比外液高. 由于离子浓度的不平衡, 神经元细胞内存在$-60mV\sim -70mV$的跨膜静息电位.
2.2 动作电位或峰电位
当神经元收到刺激时, 会发生如下事件:
- $Na^+$迅速流入, 造成静息电位升高
- $K^+$通道打开, 外流使膜电位下降.
- $Na-K$通道慢慢搬运, 使不均衡的浓度再次出现
这种电位的快速上升和下降的现象就被称为动作电位或者峰电位. 这是神经元间通信的主要模式.
峰电位本身波形固定, 其携带的重要信息通常为峰电位的放电率和峰电位出现的时间.
firing rate: 放电率, 每秒钟出现的峰电位数量
2.3 树突与轴突
细胞体连接带分支的树形结构称为树突, 其中较长的一个分支称为轴突.
许多轴突被髓磷脂覆盖, 能够显著提高峰电位长距离传输的速度.
白质由连接大脑不同区域的带髓鞘的轴突聚集而成, 而灰质主要由细胞体聚集而成.
2.4 突触
神经元间通过称为突触的连接进行交流. 当突触前神经元产生的动作电位到达突触间隙时, 会向间隙释放神经递质.
从而改变突触后细胞的局部膜电位. 可能是兴奋(excitatory), 也可能是抑制(inhibitory).
2.5 峰电位产生
其产生是一个很复杂的过程, 但在模型上可以简化成一个阈值传输的模块.
虽然这种抽象会丢失很多关于神经元的特点, 但是其在神经网络中足够有效.
2.6 神经连接的调节: 突触可塑性
大脑适应能力的关键来源就在于神经元可以通过突触可塑性来改变神经之间的连接强度和方式.
- 长时程增强: Long-term potentiation LTP
- 两个神经元之间的放电活动能够增强两者之间突触的连接强度
- 长时程抑制: Long-term depression LTD
- 不相关的放电抑制突触强度
- STDP: spike timing dependent plasticity
- 对突触前和突触后峰电位的精确时间控制能够确定突触强度的增强和抑制
此外还有短期的一些激励和抑制.
2.7 大脑组织、解剖学结构和功能
人类的神经系统可以大致分为:
- 中枢神经系统 central nervous system CNS
- 由大脑和脊髓构成
- 外周神经系统 peripheral nervous system PNS
- 躯体神经系统(骨骼肌, 连接皮肤和感受器官的神经)
- 自主神经系统(呼吸, 心跳等内脏功能的神经)
大脑由不同的神经核以及分区组成, 详见下图:
- 在大脑底部, 由髓质, 脑桥和中脑共同组成脑干
- 大脑通过脑干向身体其它部位传达所有信息
- 髓质和脑桥参与基本的调节功能, 如呼吸等
- 中脑的主要组成部分为顶盖(上丘和下丘)
- 参与眼球的控制以及视觉, 听觉反射
- 小脑是位于大脑底部高度结构化的神经元网络, 负责运动的协调
- 大脑底部往上是间脑, 包括丘脑和下丘脑
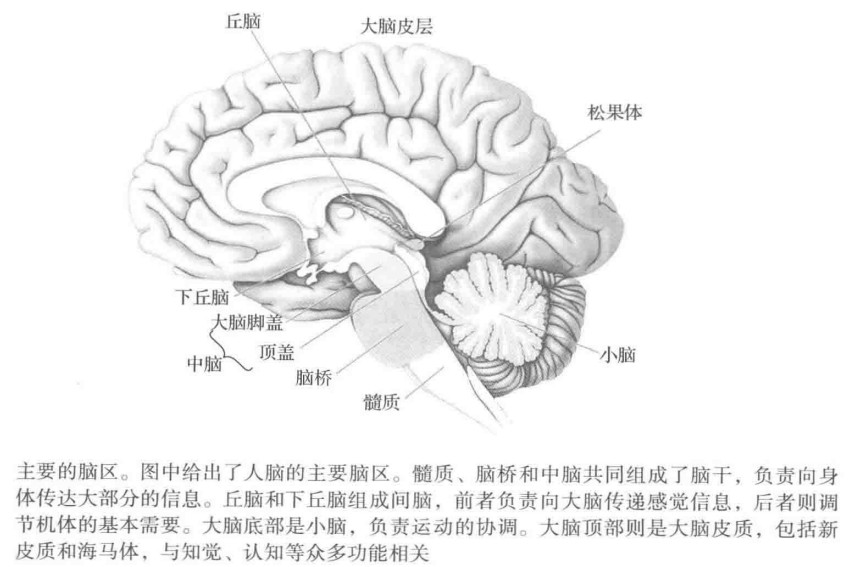
- 离大脑底部最远的是两个大脑半球, 由新皮质, 基底神经节, 杏仁核及海马体组成.
- 新皮质是位于大脑顶部有复杂沟回的区域.
- 展现出了功能特化, 如下图.
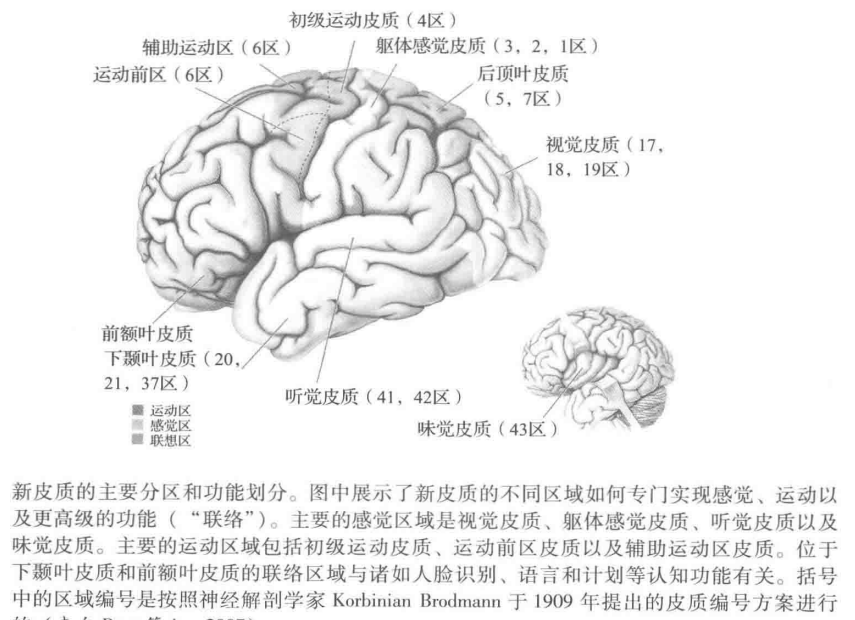
Chapter-3: 记录大脑信号和刺激大脑
3.1 记录大脑信号
3.1.1 侵入式技术
- 微电极
- 极细的导体, 由绝缘体包裹
- 测量直径约为$1\mu m$ (一个神经元的大小在几十微米的尺度)
- 细胞内记录
- 多用于脑组织切片研究
- 使用玻璃微管的膜片钳技术
- 细胞外记录
- 用微电极插入到单个神经元附近
- 多电极阵列
- 皮质脑电图
- ECoG: Electrocorticography
- 电极放置在大脑表面
- 未突破血脑屏障, 可以说是半侵入式.
3.1.2 非侵入式技术
- 脑电图
- Electroencephalography, EEG
- 主要采集大脑皮质中的电活动
- EEG记录非常适合捕捉振荡的大脑活动或多种频率的”脑电波”
- alpha波: 8-13Hz. 放松时产生
- 8-12Hz有一类特殊的称为mu节律, 当受试者不运动时, 他会出现在感觉运动区.
- beta波: 13-30Hz. 当人处于警觉或者专注状态时, 可在额叶和顶叶检测到
- delta波: 0.5-4Hz, 婴儿, 或者成人慢波睡眠时检测到
- …
- 脑磁图
- Magnetoencephalography, MEG
- 利用超导量子干涉仪测量大脑活动产生的磁场.
- 功能性核磁共振成像
- functional magnetic resonance imageing, fMRI
- 间接测量具体脑区的血流量变化.
- 功能性近红外成像
- functional near infrared, fNIR
- 类似于fMRI
- 正电子发射断层成像
- positron emission tomography, PET
3.2 刺激大脑
- 微电极
- 直接皮质电刺激
- 光刺激
- 磁刺激
- 经颅超声
3.3 同步记录和刺激
- 多电极阵列
- 神经芯片
chapter-4: 信号处理
4.1 峰电位分类
对于侵入式电极采取到的峰电位, 需要将其分离成每个电极对每个神经元采集到的峰电位信息.
4.2 频域分析
对EEG/ECoG这种整体的节律的分析, 离不开频域分析.
将时域信号分解成各个频率上的信号, 比如对mu, beta和gamma等节律的幅值和功率进行分析等.
4.2.1 傅里叶分析
TODO:
4.2.2 离散傅里叶变换
TODO:
4.2.3 FFT
TODO:
4.2.4 频谱特征
TODO:
4.3 小波分解
fourier分解的基是采用sin/cos完成的, 但是对于有限长的非周期信号, 或者是尖峰和不连续点的函数, 变换效果较差.
小波变换的基函数不再是正弦和余弦函数, 而是有限长的, 称为小波的函数.
小波是通过一个有限长的母小波经过伸缩和平移得到的.
TODO:
4.4 时域分析
4.4.1 Hjorth参数
Hjorth参数是一种用于描述信号特征的一组参数,常用于信号处理和生物医学工程领域。这些参数由瑞典神经科学家Björn Hjorth在20世纪70年代提出,用于表征生物电信号(如脑电图EEG、肌电图EMG等)的时间域特征。
Hjorth参数主要包括三个参数:
- Activity(活动度):活动度是信号的总能量或总功率,它反映了信号的总体振幅。计算活动度时,首先需要计算信号的方差(即信号的均方差),然后取方差的平方根作为活动度。活动度越高,代表信号的总体能量越大。
- Mobility(移动性):移动性描述信号的频率特性,它是信号的标准差除以信号的均值。移动性可以反映信号的频率范围。当信号的移动性较高时,表示信号的频率变化较大,即信号在不同频率上有较好的分布。
- Complexity(复杂性):复杂性是信号的移动性的标准差除以信号的移动性。复杂性参数反映了信号的波形的不规则性和复杂程度。当信号的复杂性较高时,说明信号在频率上有更大的变化。
总结一下, 用$a_0$表示所测量时段内信号的方差, $a_2$表示信号一阶导数的方差, $a_4$表示信号二阶导数的方差. 则有:
- 活动度(Activity):信号的总体振幅,与信号的方差相关。 \(A = a_0\)
- 移动性(Mobility):信号的频率特性,与信号的标准差和均值相关。 \(M = \sqrt{\frac{a_2}{a_0}}\)
- 复杂性(Complexity):信号的波形复杂程度,与信号的移动性的标准差和均值相关。 \(C = \sqrt{\frac{a_4}{a_0}}\)
这些参数在分析生物电信号的时域特征时非常有用,例如用于区分不同的脑电节律、评估肌肉运动特性等。Hjorth参数可以在生物医学工程、神经科学和生物信号处理等领域发挥重要作用。
4.4.2 分形维数
分形维数是一个用于描述分形几何结构复杂程度的概念。分形是一类特殊的几何形状,其具有自相似性(self-similarity)和自同态性(scale invariance),即它们在各个尺度上看起来都类似,并且无论如何缩放都保持其形态。分形几何在自然界、科学和艺术中都有广泛的应用。
常见的例子包括分形树、分形海岸线、分形曲线(如科赫雪花)、曼德勃罗特集等。
在分形几何中,我们用分形维数来量化这种自相似性和自同态性。分形维数是一种非整数维度,它可以是小数,表征了一个分形结构在空间中所占的空间范围。
有多种方法可以计算分形维数,其中最常用的方法之一是盒计数法(Box Counting Method)。该方法通过将分形结构用一系列盒子(或网格)覆盖,并计算所需的最小盒子数来估计分形维数。
下面是盒计数法的基本步骤:
- 将分形对象用一个固定大小的盒子(网格)进行覆盖。
- 统计所需的最小盒子数,这些盒子至少覆盖了分形对象的一部分。
- 缩小盒子的大小,并重复步骤1和2。
- 根据盒子的大小和所需的盒子数,用线性回归或其他方法来估计分形维数。
分形维数是一个重要的概念,它在自然界、图像处理、信号处理等领域具有广泛的应用。例如,在分析复杂自然物体的结构、图像压缩、分析时间序列数据的自相似性等方面都可以用到分形维数。分形维数的引入使得我们能够更好地理解和量化自然界中复杂的形态和结构。
4.4.3 自回归模型
基础: 自然信号在时间上有着相关联的趋势.
因此能够使用之前的测量量来预测下一个测量量.
自回归模型(Autoregressive Model)是一种常见的时间序列预测方法,用于分析时间序列数据的内在结构和模式。在自回归模型中,当前时间步的观测值被视为过去若干时间步的线性组合,这些过去的时间步数据被称为自回归项。
自回归模型的一般形式可以表示为:
[ x_t = c + \sum_{i=1}^{p} \phi_i x_{t-i} + \varepsilon_t ]
其中,( x_t ) 是时间步 ( t ) 的观测值,( c ) 是常数(截距),( p ) 是自回归的阶数(即使用过去多少时间步的数据),( \phi_i ) 是对应于第 ( i ) 个自回归项的系数,( \varepsilon_t ) 是误差项,表示模型无法完全捕捉的随机噪声。
在自回归模型中,( p ) 决定了模型的历史信息使用范围。较小的 ( p ) 表示模型仅使用较近的历史数据进行预测,而较大的 ( p ) 则表示模型会考虑更久远的历史数据。选择合适的 ( p ) 值对于模型的性能至关重要,通常需要通过模型评估和调参来确定。
自回归模型通常假设时间序列是平稳的,即统计特性在时间上不发生明显变化。如果时间序列不是平稳的,通常会进行差分处理(差分运算)来使其平稳,然后再应用自回归模型。
自回归模型的参数估计通常使用最小二乘法或最大似然估计等方法进行。对于给定的时间序列数据,可以通过拟合自回归模型来预测未来的数据点,也可以用于分析时间序列的特性、检测异常值等。
自回归模型的一种特殊情况是一阶自回归模型(AR(1) 模型),其形式为:
[ x_t = c + \phi x_{t-1} + \varepsilon_t ]
其中,( \phi ) 是自回归系数,表示当前观测值和前一个观测值之间的线性关系。
总结来说,自回归模型是一种基于时间序列自身过去观测值进行预测的方法,可以用于预测未来数据、分析时间序列的内在结构和模式,并在多个领域中有广泛的应用。
4.4.4 贝叶斯滤波
前面的方法基本没有保持信号的不确定性,而这其实很重要。
假设i时刻测得的数据为$y_i$, 并且已知到目前为止所有的测量值, 希望之后未知事件x的后验概率$P(x\mid y_1,\dots,y_t)$, 通过贝叶斯法则得到:
\[P(x\mid y_1,\dots,y_t) = \frac{P(x, y_1,\dots,y_t)}{P(y_1,\dots,y_t)}\\ = \frac{P(y_t\mid x, y_1,\dots,y_{t-1})P(x, y_1,\dots,y_{t-1})}{P(y_t\mid y_1,\dots,y_{t-1})P(y_1,\dots,y_{t-1})}\\ = \frac{P(y_t\mid x, y_1,\dots,y_{t-1})P(x\mid y_1,\dots,y_{t-1})}{P(y_t\mid y_1,\dots,y_{t-1})}\]考虑y对之前时刻的独立性有:
\[P(x\mid y_1,\dots,y_t) = \frac{P(y_t\mid x)P(x\mid y_1,\dots,y_{t-1})}{P(y_t\mid y_1,\dots,y_{t-1})}\]也就成为了预测-更新模型.
如果假设$x$的变化是马尔可夫过程, 则有:
\[P(x_t\mid y_1,\dots,y_t) = \Alpha P(y_t\mid x_t)P(x_t\mid y_1,\dots,y_{t-1})\\ = \Alpha P(y_t\mid x_t)\sum_{x_{t-1}} P(x_t, x_{t-1}\mid y_1,\dots,y_{t-1})\\ = \Alpha P(y_t\mid x_t)\sum_{x_{t-1}} P(x_t, x_{t-1})P(x_{t-1}\mid y_1,\dots,y_{t-1})\]4.4.5 卡尔曼滤波
假设动态概率和测量概率均为线性高斯模型:
\[x_t = Ax_{t-1} + n_t\\ y_t = By_{t-1} + m_t\]则知道: \(P(x_t\mid x_{t-1}) = N(Ax_{t-1}, Q)\\ P(y_t\mid y_{t-1}) = N(By_{t-1}, R)\)
从而贝叶斯中的各式子都可以用高斯分布来计算.
4.4.6 粒子滤波
粒子滤波也是基于贝叶斯滤波器, 不过粒子滤波器通过一群样本粒子来获取后验概率$P(x_t\mid y_1,\dots,y_{t-1})$
4.5 空间滤波
4.5.1 双极, 拉普拉斯和共同平均参考
- 双极: 两个感兴趣通道的差值
- 拉普拉斯滤波: i电极减去四个正交电极的平均值
- 共同平均参考: 减去所有信号平均值
4.5.2 主成分分析
PCA: TODO
4.5.3 独立分量分析
4.5.4 共空间模式
4.6 伪迹去除
- 阈值法
- 陷波
- PCA
chapter-5: 机器学习
暂略
chapter-6: 构建BCI
6.1 BCI分类
可以把BCI主要分成三种类型:
- 侵入式BCI
- 半侵入式BCI
- 非侵入式BCI
每类BCI还可以进一步划分成: 记录, 刺激和两种都行的.
6.2 对于构建BCI有用的反应
- 条件反射
- 集群行为
- 想象运动
- 刺激诱发行为
日志-log
2023/8/2: 写完第一版, 但是漏了很多东西没有补充, 之后再补充.