1 计算机发展历程
1.1 四个时代
1946-1957:电子管时代;
1958-1964:晶体管时代;
1965-1971:中小规模集成电路;
1972- :超大规模集成电路。
1.2 计算机分类
- SISD:单指令流和单数据流系统,传统冯诺依曼结构。
- SIMD:单指令流和多数据流系统,阵列处理器或向量处理器系统
- MISD:多指令流和单数据流系统,不存在
- MIMD:多指令流和多数据流系统,多处理器或多计算机系统。
1.3 计算机系统
- 视角1
数据库管理系统DBMS是位于用户和操作系统之间的一层数据管理软件,属于系统软件;而数据库系统DBS是指计算机系统中引入数据库后的系统。
- 视角2:五层微机
高级语言$\to$汇编语言$\to$OS$\to$机器语言$\to$微指令执行
通常将高级语言程序翻译成机器语言程序的软件叫做翻译程序。他一般是两种模式:
- 编译程序:一次编译所有,转换成exe
- 解释程序:逐条语句解释,每一次都需要翻译。
1.4 计算机组成和计算机体系结构
计算机体系结构指的是那些能够被程序所能见到的计算机系统的属性,即概念性的结构和功能特性。
计算机组成则是指如何实现计算机体系结构所体现的属性。
2 计算机基本组成
2.1 冯诺依曼机的特点
- 计算机由运算器、存储器、控制器、输入设备、输出设备五大部件组成。(此处可将输入输出设备看作一个整体,故冯诺依曼结构也可以说是由四大部件组成。)
- 指令和数据以同等地位存放于存储器(二进制存储)内,并可按地址寻访。
- 指令由操作码和地址码组成
- 指令在存储器内按顺序存放
- 机器以运算器为中心,输入输出设备与存储器间的数据通过运算器完成。
但随着现代CPU的高速发展,IO成了最大短板,所以现代计算机已经发展成以存储器为中心,使IO操作尽可能绕过CPU。
2.2 现代计算机细化框图
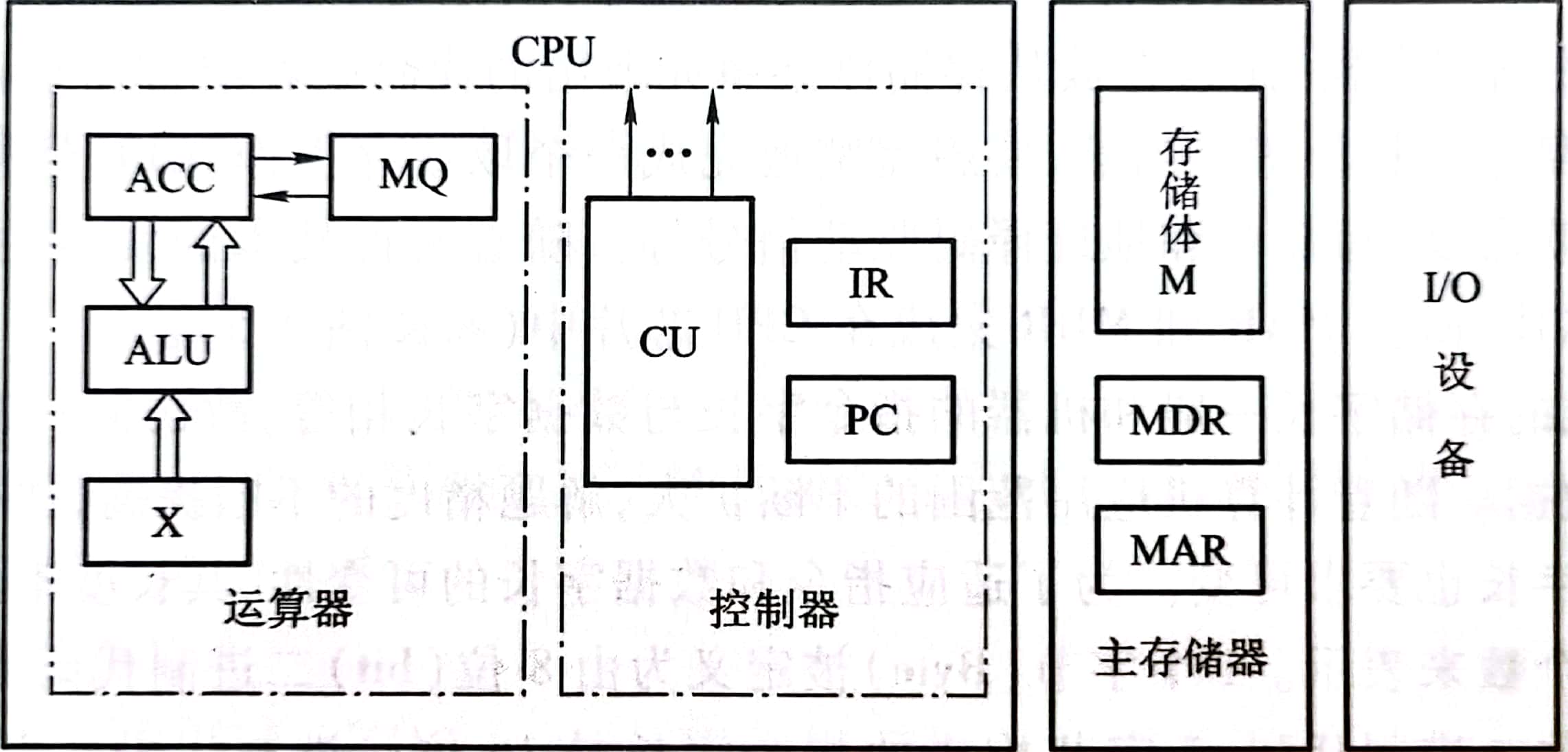
- 运算器ALU:
| 加法 | 减法 | 乘法 | 除法 | |
|---|---|---|---|---|
| ACC | 被加数、和 | 被减数、差 | 乘积高位 | 被除数、余数 |
| MQ | 乘数、乘积低位 | 商 | ||
| X | 加数 | 减数 | 被乘数 | 除数 |
- 控制器CU:
程序计数器PC:用来存放当前欲执行的指令地址,他与MAR有一条直接通路,且具有自动+1的功能。
指令寄存器IR:存放当前指令。
控制单元CU:发号施令。
- 存储器:
分为主存和辅存,为内存储器和外部存储器。值得一提的是MAR和MDR
MAR是用来存储访存地址。MDR是用来暂时存储要从M中读或者写的信息。
CPU包括MAR、MDR、PC、IR、ALU、GPRs等
2.3 指令执行过程的描述
- 取址:PC$\to$MAR$\to$M$\to$MDR$\to$IR 这个过程是基本不变的
3 计算机技术指标
3.1 机器字长
机器字长是指CPU一次能处理数据的位数。
3.2 存储容量
包括主存和辅存,前者通常用总位数,后者通常用字节数。
3.3 运算速度
吉普赛法:
\[T_M=\sum_{i=1}^n f_it_i\]即考虑每条指令的执行时间以及它们在全部操作中所占比例,借此来衡量运行速度。
另外也可以使用CPI(Cycle Per Instruction)或者MIPS(Million Instruction Per Second)来衡量。
计算机的应用十分广泛,但无论在什么地方,信息在机器内部的表示形式都是一致的。这一篇笔记旨在介绍计算机内数的一般表示法,以及运算规律。
4 有符号数与无符号数
有无符号是指正负,如果数据的每一位均表示大小,那么负数便无法表述。
4.1 无符号数
所谓无符号数,就是没有符号位的数码。其中每一位均表示大小,那么以32位为例
其范围为0~4,294,967,295
这里需要强调的是,尽管有32位,但是由于0位的存在,其最高位的权值为$2^{31}$,其值的范围为:$0\sim 2^{32}-1$. 如果此处不对其位数与幂次有一个清醒的认识,那么后续在小数部分很可能迷糊。
4.2 有符号数
先介绍一下二进制数,尤其是数值与位的关系:
| 位数 | n | 4 | 3 | 2 | 1 | -1 | -2 | -m |
|---|---|---|---|---|---|---|---|---|
| 值 | $2^{n-1}$ | $2^3$ | $2^2$ | $2^1$ | $2^0$ | $2^{-1}$ | $2^{-2}$ | $2^{-m}$ |
机器很难识别一个数字的正负,如果以$+/-$这样的符号表示,就需要做许多无关的编码,而且还要保证对正负号的编码在数字码系统中无前缀。这十分困难,所以直接用0代表正;1代表负数。
把符号“数字化”的数字称为机器数
这种简单粗暴的直接体现就是
4.2.1 原码表示法
原码表示法的规则就是,直接在数字前,正数补0,负数补1。
如此,32位有符号整数的表示范围就是$-2^{31}+1\sim 2^{31}-1$
对于n-1位数值位的真值$x$,原码表示有n位。其形式化定义为:
\[[x]_{原}\left\{\begin{matrix}0,x\qquad 0\le x \le 2^{n-1}-1\\2^{n-1}-x \qquad -2^{n-1}+1\le x \le 0 \end{matrix}\right.\]这里也将原码限制在n位,是为了和后面补码转换等对齐。否则很容易被真值、原码等弄混。
这里尤需要注意的一点是:原码表示法中有两个0,为‘+0’‘-0’。
小数的表示法只需要同除$2^n$即可。
虽然原码表示法和真值之间的互换十分简单方便,但是在运算上十分麻烦。这是因为自然的‘+’仅对于数值位成立,而对符号位并不成立,由此会造成困难。
换句话说,要么将‘+’从自然的无符号加法扩展为有符号加法,要么寻求编码方式的改变。
显然,对计算机来说,后者对资源的消耗会更少。这也就是补码表示法。
另外,补码也解决了减法的问题。因为减法可以理解为加上一个数的负数。
4.2.2 补码表示法
所谓补码,就是用一个数代替另一个数参加运算。
以时钟为例,由于最大小时数只是12,任何大于12的数都会自然模12从而舍去进位。
比如,从6点到3点,可以‘-3’,也可以‘+9’。由于把模数看作自动抹除的进位。
那么对于n-1位的真值$x$来说,最大值为$2^{n-1}$,故取模数$2^{n+1}$:
\[[x]_{补}\left\{\begin{matrix}0,x\qquad 0\le x \le 2^{n-1}-1\\2^n+x \pmod{2^n}\qquad -2^{n-1}+1\le x \le 0 \end{matrix}\right.\]有趣的是,根据这种表示法,‘+0’‘-0’的编码唯一了,而多余的‘1,0000’就变成了最小的负数‘-16’
但是这种定义并没有解决减法的问题,因为在定义中,如果$x$为负数,照样会有减法出现。
观察$x=-x_1x_2x_3x_4$
则:
\[[x]_{补}=2^5+x=2^5-x_1x_2x_3x_4=100000-x_1x_2x_3x_4 \\ = 0001+1111-x_1x_2x_3x_4+10000\]其中,$10000$可以写成$1,0000$充当符号位;$1111-x_1x_2x_3x_4$就是对每位取反。
综合来看,就有了“除符号位外,按位取反+1”的从原码到补码计算法了。
$1111-x_1x_2x_3x_4$可以专门定义一个取反的反码运算,但是没有必要详细定义了。
4.2.3 移码表示法
补码在比大小上,又出了很大的问题。
对n位真值$x$,不妨就直接$+2^n$把所有的负数都变成正数。
进一步观察可以发现,同一个真值的移码和补码只差一个符号位,这是因为$10000=1111+0001$。而见前一节的运算,还多出一个$10000$
5 定点、浮点表示法
5.1 定点表示法
这种表示都是固定的,无论是小数还是正数,一个数符+若干数值。
当然,这种情况下,小数点的位置是默认的。
5.2 浮点表示法
浮点表示法的核心是:阶码+尾数
另外,对尾数最高位取1的表示法称为规格化。
5.2.1 浮点表示的范围
设阶码的数值位取n位,尾数的数值位取m位。
则对正数来说,其取值范围为:$2^{-(2^n-1)}\times 2^{-m}\sim 2^{2^n-1}\times (1-2^{-m})$
对于负数来说,其取值范围为:$-2^{(2^n-1)}\times (1-2^{-m})\sim -2^{-(2^n-1)}\times 2^{-m}$
- 绝对值大了,称上溢,过小则称下溢。
另外,为了提高浮点数的精度,我们可以将尾数规格化。当基数为2时,最高位保持为1即为规格化。
5.2.2 比较与说明
- 当浮点机和定点机位数相同时,浮点数的范围更大;
- 浮点数规格化后,相对精度更高;
- 浮点数运算步骤较麻烦;
- 在溢出的判断上,浮点数是对阶码判断,而定点数只是对数值本身运算。
机器零:当一个浮点数尾数为0时,无论其阶码为何值;或者阶码等于小于它所能表示的最小数时,不管尾数为何值,都将其作为0看待。
6 定点运算
定点运算包括移位,加,减,乘,除几种;
6.1 移位
移位操作十分地重要,几乎是后续操作的基础。
其核心在于对补位的分析:
| 真值 | 码制 | 添补代码 |
| 正数 | 原码 | 0 |
| 补码 | 左移补0 | |
| 右移补1 | ||
| 反码 | 0 |
还有一种移位称为逻辑移位,它是对无符号数而言的,统一补0。
6.2 加法、减法
由于计算机的实现一般将$A-B$化成$A+(-B)$,所以加法减法本质是一致的。
减法只需要对减数做取补操作即可。唯一一个需要注意的问题是溢出,又称Overflow。
无符号数超出范围称为进位。
- 一位溢出判断
一位判断很简单,核心就是溢出的两种情况。(针对符号位)
\['0'+'0'='1';'1'+'1'='0'\]计算机中采用一位符号位判断时,通常使用数值最高有效位进位和符号进位进行异或操作。若1,则溢出;否则则无溢出。
若为正数溢出情况,易于理解;但是负数溢出,用上种判断方式有一些疑惑。如何考虑呢,只需要观察到补码和移码在数值位上的高度相似性即可。
- 两位溢出判断
两位溢出基于2符号位补码,也就是把定义中的数字在扩大2倍。
其原则为,两符号位不同则溢出。这可能有一些令人费解,尤其是对于负数溢出情况来说。不过考虑方法还是和一位溢出判断一致。
无论如何,最高位都可以作为结果的符号位;另外,两位符号位并不需要在寄存器中体现,因为正常的数字两位符号位必然是相同的,而加法器对于两位符号位几乎是必须的。
6.3 乘法
考究一下笔算乘法,我们可以把乘法拆解成加法+移位操作。

计算机很容易做这种事情,用一个寄存器放被乘数,一个寄存器放乘积的高位,一个寄存器放乘数和乘积的低位。
对于原码的乘法只需要转换成真值+符号为判断即可,十分方便。
均为逻辑右移,且部分积取$n+1$位,防止乘出大数字。
我们还可以使用两位乘增快一下手法。
核心问题在11上,对于$+3x$有些麻烦了,不妨直接$-x$,然后右移加一个$x$。那么就必须要设置一个标志位。

计算过程中尤其需要注意的是,部分积过程可能$+2x$导致部分积的绝对值大于2。所以需要取3位符号位。另外还需要在被乘数前补$1~2$个0.
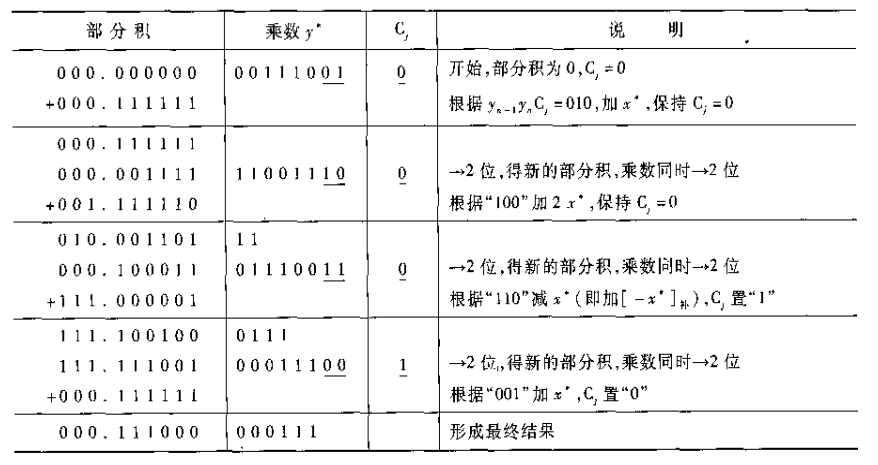
但是计算机中的有符号整数多是补码形式,为了做乘法没有必要每次都进行一次转换。
于是需要分析一下补码乘法:
- 乘数$y$符号为正
取$[x]{补}=x_0.x_1…x_n,[y]{补}=0.y_1…y_n$
则$[x]_补\cdot[y]_补=(2+x)y\equiv 2^{n+1}y+xy \equiv 2+xy\equiv [xy]_补\pmod{2}$
- 乘数$y$符号为负
有$[xy]_补=[x(1.y_1…y_n-2)]_补\equiv [x(0.y_1…y)]_补 +[-x]_补\pmod{2}$
从这中,我们可以得到booth算法
\[[xy]_补= [x]_补(0.y_1...y) -[x]_补\cdot y_0\pmod{2}\]这里使用了恒等式$[x]_补+[-x]_补\equiv 0\pmod{2}$
进一步有:
\[[xy]_补= [x]_补(0.y_1...y) -[x]_补\cdot y_0 \\ = [x]_补(-y_0+y_12^{-1}+...+y_n2^{-n}) \\ =[x]_补(y_1-y_0+(y_2-y_1)2^{-1}+...+(y_{n+1}-y_n)2^{-n})\]此处取$y_{n+1}=0$即可,所以需要特定的补位。在这种运算中,补码的符号位一起参与运算。
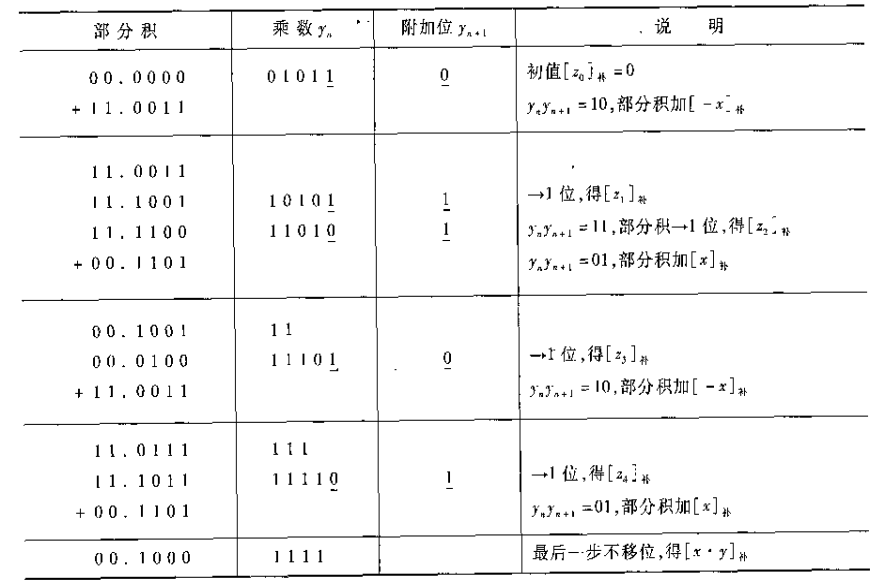
同样,我们也可以使用二位乘,不够没有必要就是了。
在这里需要指出,符号位是否自然形成,是依赖于计算过程中+号的性质。
6.4 除法
对于正常的笔算除法,我们也需要考虑试探除,否则不能确定是否上商为1.
那么这对于计算机来说就十分难受了。我们首先针对原码分析。
原码分析的核心在于余数,如果余数小于0,那么就需要把试探的1改成0.
所以就有了恢复余数除法,首先直接+$[-y]_补$,
- 如果余数为负,就$+y$补回来,然后上商0,左移一位。
- 如果余数为正,上商1,左移一位。
符号也可以直接确定。
但是这种试探运算不太漂亮,考虑其实际运算。
- 如果余数为负,就$+y$补回来,然后上商0,左移一位。等价于$2(R+y)-y=2R+y$
- 如果余数为正,上商1,左移一位。等价于$2R-y$
这就得到了加减交替法:
但是问题来到补码这儿就十分复杂了。
如何确定商值;如何得到符号位;如何获得新的余数。
对于第一个问题,我们需要比较被除数和除数的大小。
- 同号,做减法。如果余数和除数同号,够减,商0
- 异号,做加法。如果余数和除数异号,够减,商1
所以就变成了,余数和除数同号商1,否则商0;
由上述过程可知,商符是在求值的过程中自然生成的。
余数生成和加减交替法一致。
除法的全部复杂都隐含在,除数和被除数的大小比较中了。
7 浮点运算
浮点运算基于前面的方式进行:
- 对阶,使两数的小数点位置对齐;
- 尾数求和,按定点运算求和;
- 规格化,为提高精度;
- 舍入,为提高精度,要考虑尾数右移时丢失的数值位;
- 溢出判断。
7.1 对阶
对阶的原则是小阶向大阶看齐。
7.2 舍入
可以盲目补1
8 ALU
牢记进位即可:
\[C_i=A_iB_i+(A_i+B_i)C_{i-1}\]9 机器指令
一般来说,及其指令由操作码与地址码构成。
|操作码字段|地址码字段| |:–:|:–:|
9.1 操作码
操作码反映机器的行为,它的长度可以是固定的,也可以是变化的。
变化长度可以让频繁的指令使用短编码,从而降低程序的平均编码长度。但是其短板是需要更加复杂的译码器。
可变长度有一种扩展操作码技术实现,其特点是操作码的位数随地址数的减少而增加。
其核心是挑选特定地址当作固定前缀扩展。
9.2 地址码
地址码反映机器操作的范围,涉及哪些存储空间。各个指令的地址码数量从0到4个不等。
有些指令将特定寄存器“隐藏”在语句实现中,从而实现所需地址码减少。这样做一方面将地址码的范围扩大了,但另一方面也占用了某些寄存器的使用。
- 需要注意,每一次访存都是对CPU资源的浪费。
所谓改善,不过都是权衡的结果。
这里需要特别提一句,存储器映射IO设备。有的ISA将输入输出指令按设备区别特殊编码;有的ISA将这些IO口全部作为地址对待。具体优劣笔者不知。
10 操作数类型和操作类型
10.1 操作数类型
- 地址:无符号整数
- 数字:定点数、浮点数、十进制数
- 字符:ASCII
- 逻辑数:逻辑运算
存储时考虑对齐,便于CPU在一个周期内取出。
10.2 操作类型
- 数据传输
- 算术逻辑
- 移位
- 跳转
- 无条件
- 有条件
- 调用返回
- 陷阱Trappings
- IO
- 其他:包括停机、等待、空指令等。
11 寻址方式
寻址针对指令来讲,自然分成两种。
11.1 指令寻址
- 顺序 $(PC)+1\to PC$
- 跳跃 JMP
11.2 数据寻址
这个花样就比较多:
- 立即寻址(Immediate Addressing)
- 立即数为补码
- 直接寻址
- 直接给出内存地址
- 隐含寻址
- 操作数地址隐藏在某个特定寄存器中
- 间接寻址:EA = A
- 有效地址由形式地址间接提供
- 寄存器寻址
- 不访存;寄存器个数有限,可缩短指令字长
- 寄存器间接寻址
- 有效地址在寄存器中, 操作数在存储器中,执行阶段访存
- 基址寻址:EA = (BR) + A
- 指令给出A,隐含BR;可扩大寻址范围
- BR 内容由操作系统或管理程序确定;有利于多道程序
- 在程序的执行过程中 BR 内容不变,形式地址 A 可变、
- 变址寻址:EA = (IX) + A
- IX 的内容由用户给定;便于处理数组问题
- 在程序的执行过程中 IX 内容可变,形式地址 A 不变
- 相对寻址:EA = (PC) + A
- A 是相对于当前指令的位移量(可正可负,补码)
- 程序浮动;广泛用于转移指令
- 堆栈寻址
- 硬堆栈:多个寄存器
- 软堆栈;指定的存储空间
Linux的堆栈是。。。
12 指令格式举例
设计时的考量:
- 指令系统的 兼容性:Intel的历史包袱
- 其他类型:
- 操作类型
13 RISC 技术
产生缘由:典型程序中 80% 的语句仅仅使用处理机中 20% 的指令
13.1 主要特征
- 选用使用频度较高的一些 简单指令,复杂指令的功能由简单指令来组合
- 指令 长度固定、指令格式种类少、寻址方式少
- 只有 LOAD / STORE 指令访存
- CPU 中有多个 通用 寄存器
- 采用 流水技术 一个时钟周期 内完成一条指令
- 采用 组合逻辑 实现控制器
- 采用 优化 的 编译 程序
13.2 CSIC的主要特征
- 指令系统 复杂庞大,各种指令使用频度相差大
- 指令 长度不固定、指令格式种类多、寻址方式多
- 访存 指令 不受限制
- CPU 中设有 专用寄存器
- 大多数指令需要 多个时钟周期 执行完毕
- 采用 微程序 控制器
- 难以 用 优化编译 生成高效的目的代码
13.3 对比
- RISC更能 充分利用 VLSI 芯片的面积
- RISC 更能 提高计算机运算速度
- RISC 便于设计,可 降低成本,提高 可靠性
- RISC 有利于编译程序代码优化
- RISC 不易 实现 指令系统兼容