吴恩达机器学习课笔记
1 Linear Regression
1.1 A specific problem
首先来看一个具体的问题,房价与房屋面积:
| 面积 | 总价格(万) |
|---|---|
| 404 | 500 |
| 376 | 425 |
| 86 | 110 |
| 310 | 360 |
| 153 | 180 |
| … | … |
| 163 | 189 |
给定数据集,我们试图在给定面积的情况下尽可能找到一个模型。我们输入面积,它给出房价。定义$x^{(i)}$为第i项数据的面积.
该问题可用监督学习解决,我们来看看这个模型在干些什么。
- 从训练集中提取出特征和目的
- 给定学习算法
- 建立模型$f(x)=\hat{y}$
1.2 How to represent $f$?
初步看来,我们坚信该模型是一条直线,有:
\[f_{w,b}(x)=wx+b\]这就是Univariate Linear Regression。
1.3 Cost Function
要实现学习算法, 我们必须依赖一个成为损失函数的东西. 损失函数会告诉我们, 该模型当前如何, 以便于我们更好地改进它.
回顾之前的模型:
\[f_{w,b}(x)=wx+b\]$w,b$称为parameter, coefficients, weights等. 显然, 这些参数的更改会造成模型之间的差异. 同样的, 我们可以假设出一个最优模型出来, 并衡量当前模型同最优模型之间的差异, 并不断优化当前模型.
就线性回归模型来说, Square Error Cost Function工作得足够好:
\[J(w,b) = \frac{1}{2m}\sum_{i=1}^m(\hat{y}^{(i)} - {y^{(i)}})^2\]其中$\hat{y}^{(i)} = wx^{(i)}+b$, 由于训练集中数据已给定, 所有x和y均已知, 则该函数实际上是$w,b$的函数, 选取不同的参数会让该函数值变化. $m$是数据集的大小.
我们如何从这种变化中选定学习的方法和方向呢? 损失函数又能告诉我们什么?
1.4 Cost Function Intuition
接下来通过可视化来建立对损失函数的直觉.
首先清点一下我们已有的东西:
- model:$f_{w,b}(x)=wx+b$
- parameters: w,b
- cost function: $J(w,b) = \frac{1}{2m}\sum_{i=1}^m(f_{w,b}(x) - {y^{(i)}})^2$
- goal: $\min_{w,b}J(w,b)$
损失函数在告诉我们, 当前参数下, 这个模型和真实值的差距. 所以我们的目的就是使损失函数尽可能小. 当$J=0$时, 在已有训练集上的每一个点, 模型都给出和实际一致的值.
首先分析一下损失函数, 固定$b$得到:
\[J(w) = \frac{1}{2m}\sum_{i=1}^m(wx^{(i)} + b - {y^{(i)}})^2\]对$w$来说, 这是一个二次函数. 而对$b$来说, 也是如此. 事实上, 我们可以通过最小二乘法直接得到最佳的$w,b$.
接下来用图来更直观的表示出它的形状, 和我们的目的地:
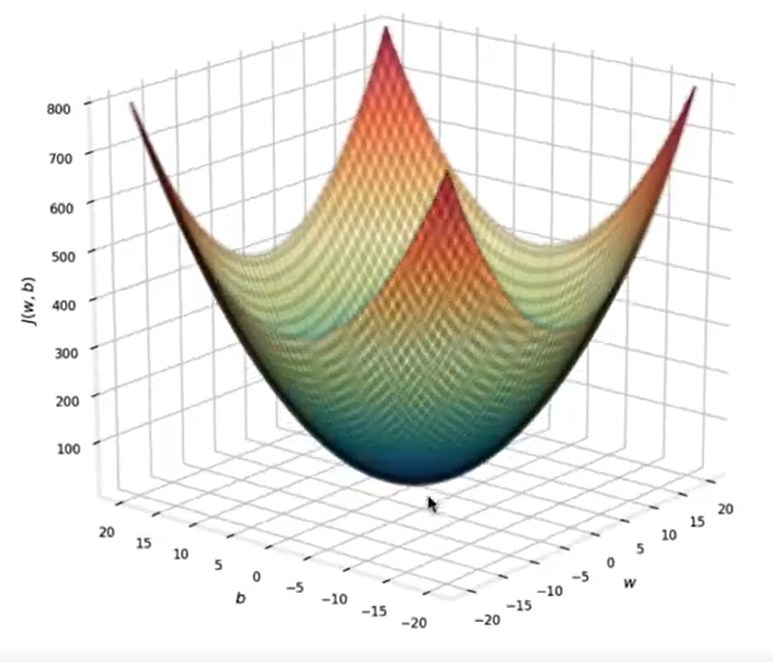
我们会从碗壁上的点开始, 达到碗底, 也就是我们接下来要做的.
1.5 Gradient Descent
本节的目的是未来最小化代价函数.
其实际过程就是随机选定一点, 然后朝最陡的方向前进. 不断更新$w,b$:
- $w = w - \alpha \frac{\partial}{\partial w} J(w,b)$
- $b = b - \alpha \frac{\partial}{\partial b} J(w,b)$
注意同步更新, 即w和b的更新是同步的, b的更新不会使用w的新值.
其中$\alpha$是学习率, 可以理解为每次更新的步长.
其中后半部分的理解可以由简化的二次函数理解, 减号总会造成参数向最小函数值移动.
梯度下降算法终止于最小值点:
- 偏导数为0
- 每次更新后, 损失函数变化已经很小了
注意到函数可能有多个极小值点, 所以单一的凸函数是绝佳选择
1.6 Learning Rate
如果$\alpha$太小, 则需要过多步骤才能抵达最小值点; 如果$\alpha$太大, 则可能造成损失函数变大, 大家可以通过二次函数理解, 图以后可能补上.
在算法运行的初始阶段, 可以将学习率设小, 只要观测到每次更新后, 损失函数逐渐变小则可暂时认为代码中无bug.
最后我们来补上偏导数如何计算:
已知: \(J(w,b) = \frac{1}{2m}\sum_{i=1}^m(f_{w,b}(x^{(i)}) - {y^{(i)}})^2\)
有: \(\frac{\partial}{\partial w} J(w,b) = \frac{1}{m}\sum_{i=1}^m(f_{w,b}(x^{(i)}) - {y^{(i)}})x^{(i)} \\ \frac{\partial}{\partial b} J(w,b) = \frac{1}{m}\sum_{i=1}^m(f_{w,b}(x^{(i)}) - {y^{(i)}})\)
2 LR with Multiple Variables
对于数据集中更多的特征, 单一的$x$很难满足我们的需求. 比如房屋离市中心的距离, 层数等也会影响房价. 我们使用$x_j$代表数据项的第j项特征. $\vec{x}^{(i)}$代表第i项数据的特征集合, $\vec{x}^{(i)}_j$代表第i项数据的第j项特征.
定义点积和向量后, 可以更新模型如下:
\[f_{\vec{w},b}(\vec{x}) = \vec{w}\cdot\vec{x}+b\]基于该模型的学习算法称为多元线性回归;
2.1 Vectorization
对于向量(或矩阵), 各种框架会利用矢量运算部件进行优化, 从而达到比循环更优的效率.
2.2 Gradient Descent
过程基本一致, 对$\vec{w}$略有更新:
\[w_j = w_j - \alpha \frac{\partial}{\partial w_j} J(\vec{w},b) \\ \frac{\partial}{\partial w_j} J(\vec{w},b) = \frac{1}{m}\sum_{i=1}^m(f_{\vec{w},b}(\vec{x}^{(i)}) - {y^{(i)}})x_j^{(i)}\]2.3 Feature Scaling
仍然采用房价, 房屋面积可能在100这个量级, 但是离市中心距离则跨度非常之大, 对这两个变量的参数$w$, 前者可能会比较大, 而后者比较小. 那么采用相同的学习率下, 后者迅速达到稳定, 而前者则可能需要更多步骤才能达到稳定.
所以通过缩放特征到相对平衡的情况会比较好. 下面说几种实际的方法:
- 最大值, 直接除以最大的绝对值放缩在[-1,1]
- 平均值, 减去平均值后除以极差
- Z-core, 减去平均值后除以标准差
说不上哪个更好, 只能说别让特征之间差距太大.
3 Classification
对于分类问题, 线性回归绝对不是一个好算法. 这将引出逻辑回归算法, 如今在分类问题中广泛运用.
3.1 Logistic Regression
线性回归在有较大偏离值的数据集中容易偏离, 从而对于聚集于中心的例子会给出错误判断.
我们需要某种方式”平滑”线性回归后的式子. 通常来说, Sigmoid函数不错:
\[g(z) = \frac{1}{1+e^{-z}}\]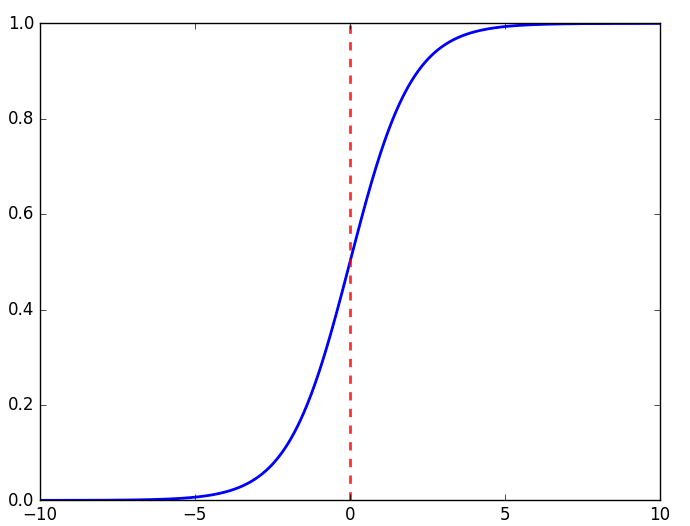
我们令$z = \vec{w}\cdot\vec{x}+b$替换得到:
\[f_{\vec{w},b}(\vec{x}) = g(\vec{w}\cdot\vec{x}+b) = \frac{1}{1+e^{-(\vec{w}\cdot\vec{x}+b)}}\]它最终会输出一个(0,1)之间的值, 可以理解为概率, 更”概率”的表达如下:
\[f_{\vec{w},b}(\vec{x}) = P(y=1\mid \vec{x}; \vec{w},b)\]即在给定输入$\vec{x}$, 参数$\vec{w},b$的条件下, $y=1$的概率.
3.2 Decision Boundary
对于最终给定的概率, 我们该如何给出模型的答案呢?
就是设定一个界限, 当取值大于0.5时, 我们认为$\hat{y} = 1$
3.3 Cost Function
首先看已知的损失函数:
\[J(\vec{w},b) = \frac{1}{m}\sum_{i=1}^m\frac{1}{2}(f_{\vec{w},b}(\vec{x}^{(i)}) - {y^{(i)}})^2\]一般地, 定义损失loss为预测值和实际值之间的差距 $L(f_{\vec{w},b}(x^{(i)}),{y^{(i)}})$. 从而得到一般的损失函数定义:
\[J(\vec{w},b) = \frac{1}{m}\sum_{i=1}^mL(f_{\vec{w},b}(\vec{x}^{(i)}),{y^{(i)}})\]在线性回归中, 它为:
\[L(f_{\vec{w},b}(\vec{x}^{(i)}),{y^{(i)}}) = \frac{1}{2}(f_{\vec{w},b}(\vec{x}^{(i)}) - {y^{(i)}})^2\]在逻辑回归中, 由于采取Square Error Cost Function后, 得到的损失函数不满足凸性, 所以我们得选择另一个足够好的.
考虑到01处使得正确值的损失函数尽可能小, 于是有:
\[L(f_{\vec{w},b}(\vec{x}^{(i)}),{y^{(i)}}) = -y^{(i)}\log(f_{\vec{w},b}(\vec{x}^{(i)})) - (1 - {y^{(i)}})\log(1-f_{\vec{w},b}(\vec{x}^{(i)}))\]如果y=0, 则后项起作用; 如果y=1, 则前项起作用.
求偏导后发现和线性回归的式子在形式上一致.
3.4 Overfitting
事实上, 给定数据集, 总可以使用拉格朗日插值法得到一个完美符合的函数模型. 但是这样的结果是该模型对于训练集之外的数据表现十分差.
我们的学习算法很可能会为了更小的损失函数而滑向这个完美的函数模型, 这就称为过拟合.
如何解决它呢?
- 收集更多数据
- 选择更多的特征, 或者减少特征
- 正则化
我们详细讨论最后一种
3.5 Regularization
修改成本函数, 抑制影响较大的feature参数, 比如加上$1000w_i^2$.
从而有正则项:
\[\frac{\lambda}{2m}\sum_{j=1}^nw_j^2\]加在损失函数上后, 重新求导后即可.