KMP算法

KMP是三位大牛：D.E.Knuth、J.H.Morris和V.R.Pratt同时发现的。它的核心就是充分利用了已知的匹配信息。

KMP算法要解决的问题就是在主串中模式串(pattern)的定位问题。

比如在ABCD中寻找BC，这里找到了，返回位置1；寻找DF，没找到，返回-1.

模式串定位问题应用是如此之广泛(比如浏览器、文本编辑器等都支持的搜索功能)，以至于普通的暴力搜索办法的效率，已经不够了。

问题描述

为了更方便讨论，我们对问题进行定义。

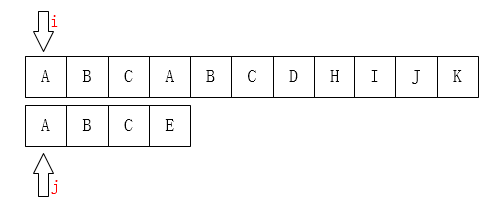
我们的目的是在母串或者主串(后称为M)中寻找模式串或者子串(后称p)。

为方便我们描述算法，定义M的指针i，p的指针j，用来讨论当前比较的字符。

如下图：

首先看暴力搜索算法.

暴力搜索算法-BF

对于这个问题，有一个自然的想法：

我们只需要从M串的第一个开始，与p匹配，成功就返回；失败就从母串的第二个开始，逐渐匹配。

代码如下：

#include<stdio.h>
#include<string.h>

char M[] = "I would kill you!";
char p[] = "ould";
int cnt = 0;

int BF_find(char[], char[]);

int main()
{
	int flag = BF_find(M,p); 
	printf("%d\n cnt:%d",flag, cnt);
	return 0;
} 

int BF_find(char mother[], char pattern[])
{
	int flag = -1;
	int len = strlen(mother);
	int plen = strlen(pattern);
	//printf("5:%d\n",plen);
	int i,j;
	for(int k = 0; k <= len-plen; k++)
	{
		i = k; flag = i;
		for(j=0; j < plen; j++,i++)
		{
			cnt++;//记录比较次数 
			if(pattern[j] == mother[i]) ;
			else{
				flag = -1;
				break;
			}
		}
		if(flag != -1) break;
	}
	return flag;
}

当然，也有和KMP思想更接近的算法，也就是把i指针回退表现得更加明显的算法。来自孤~影

char M[] = "I would kill you!";
char p[] = "ould";
int cnt = 0;

int BF_find(char mother[], char pattern[])
{
	int i = 0; // 主串的位置
	int j = 0; // 模式串问题
	int mlen = strlen(mother);
	int plen = strlen(pattern);
	
	while(i < mlen && j < plen)
	{
		if(++cnt && mother[i] == pattern[j])
		{
			i++;j++;//两者相同，比较下一个 
		}else{// 两者不等，j回退为0，i指针回退 
			i = i-j+1;
			j = 0;
		}
	}
	if(j == plen)
		return i-j;
	else
		return -1;
}

我们可以看出，暴力算法的核心就是每次不等时，就会把i指针回溯。

我们看串M=SSSSSSSSSSSS中找p=SSSSB，它需要比较44次才可以给出结果。

有没有一种可能，我们可能尽量保持i指针不动呢？因为这个时候，我们已经知道前四个位置都是匹配的了。

KMP算法

综上得到KMP算法的核心：利用已经部分匹配的有效信息，保持i指针不回溯，通过修改j指针，让模式串尽量地移动到有效的位置

1 寻找有效的位置

看如下几种情况：

   i
abacddd
abae
   j

此时我们如何调整j指针的位置呢？我们是不是直接可以将j挪动到p[1]，也就是：

   i
abacddd
  abae
   j

为什么呀！因为我们知道a和a是已经匹配好了的。

再看复杂一点的：

      i
abcdabcdefghijk
abcdabd
      j

调整为：

      i
abcdabcdefghijk
    abcdabd
      j

我们可以看出一些端倪。

跳转的前提是一下两端字符相等：

当i和j前的k个字符
p串最前端的k个字符

换句话说，对于情况M[i]!=p[j]，我们单独考察模式串p[0]~p[j-1]这个子串的一截。

这一截子串的前k个字符和后k个字符串相同。

用下面表格来表示：

0	k-1	k	…	j-k	j-1	j
a	b	c	d	a	b	d

ab就是那k个字符。

所以我们需要考察串p[0]~p[j-1]的最长相同前缀和后缀。

其后缀保证了母串i指针前的k个字符是什么；前缀保证了转移以后的j指针前k个字符和母串i指针前k个字符是相等的。

而这种考察是只和子串相关的。

所以KMP算法的核心就是找到j回溯的位置。也就是将j=0替换成j=next[j]，next[j]中保存了j下一次回溯的位置。

而上文中的k就是我们需要的next[j]

下一步的核心就变成了求解模式串p的next[]数组。

2 计算回溯数组

直接上代码：

void getNext(char pattern[])
{// next[]定义在全局
    int len = strlen(pattern);
    next[0] = -1;
    int j = 0;
    int k = -1;
    while (j < len - 1) {
        if (k == -1 || pattern[j] == pattern[k]) {
            next[++j] = ++k;
        } else {
            k = next[k];
        }
    }
}

接下来我们逐渐解释这个算法：

对于j=0，不匹配没有什么办法，不可能再移动。

对应初始化next[0] = -1;

进入j=1的情况，不匹配也就只能为0了

也就是第一次执行next[++j] = ++k;，也就是next[1] = 0;

之后的情况就有些迷人了，不过我们先解释k，j的含义。

j就是当前指针，而k是指向跳转的指针。在++j和++k后，再次进入判断pattern[j] == pattern[k]。如果相等，那么

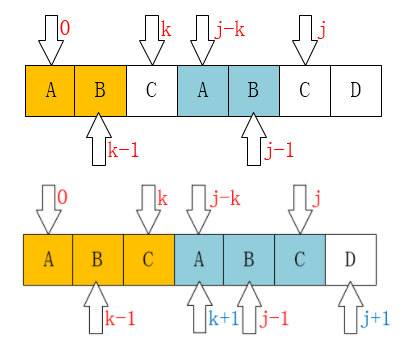
这是因为从j和k开始数到现在都是相等的，自然可以把这个相等的符号加入。

也就是p[0]~p[k-1]+p[k]与p[j-k]~p[j-1]+p[j]是一致的，所以就有next[++j] = ++k;

接下来解释这个else的部分，这是最反直觉的地方。它核心就是当p[k]!=p[j]，我们突然调整了k指针，为什么调整k指针呢？

其实，这相当于一个递归调用，或者说是所谓的动态规划。这个时候，当前的k已经无法找到与j指针相匹配的内容，那么我们就找上一级，也就是上一个和k指针指向位置的，具有相同字符串的地方。

更直观一点的说法是，我们在next数组的求解中，使用了KMP的算法思想。其实next的计算过程本质也是一次KMP匹配，不过是自身对自身的匹配。

我目前的理解，也只能做出如此的解释了。

全代码如下：

#include<stdio.h>
#include<string.h>

char M[] = "SSSSSSSSSSSS";
char p[] = "SSSSB";
int cnt = 0;

int KMP_find(char[], char[], int[]);
void getNext(char pattern[], int[]);

int main()
{
	int len = strlen(p);
    int next[len];
	getNext(p,next);
	for(int m=0; m<len; m++)
		printf("%d ",next[m]);
	int flag = KMP_find(M,p,next); 
	printf("%d\n cnt:%d",flag, cnt);
	return 0;
} 

int KMP_find(char mother[], char pattern[],int next[])
{
	int i = 0; // 主串的位置
	int j = 0; // 模式串问题
	int mlen = strlen(mother);
	int plen = strlen(pattern);
	
	while(i < mlen && j < plen)
	{
		if(++cnt && (mother[i] == pattern[j] || j == -1) )//这里是为了防止j反复跳转，出现问题。
		{
			i++;j++;//两者相同，比较下一个 
		}else{// 两者不等
			//i = i-j+1;i指针不回退 
			j = next[j];// j回退为next[j]
		}
	}
	if(j == plen)
		return i-j;
	else
		return -1;
}

void getNext(char pattern[], int next[]) 
{
    int len = strlen(pattern);
    next[0] = -1;
	int j = 0;
    int k = -1;
    while (j < len - 1) {
        if (k == -1 || pattern[j] == pattern[k]) {
            next[++j] = ++k;
        } else {
            k = next[k];
        }
    }
}

对那个诡异的串，从44次降为20次。可以看到，对于高度相似的串，效率提高是十分快速的。

这里没有对next数组的求解计算比较，当然也可以加上。问题不大。

3 进一步优化

if (k == -1 || p[j] == p[k]) {
   if (p[++j] == p[++k]) { // 当两个字符相等时要跳过
      next[j] = next[k];
   } else {
      next[j] = k;
   }
}else ...

这里就是对转移之后的下一个符号做判断。

感谢孤~影

还有两篇类似的： KMP算法详解-彻底清楚了(转载+部分原创) KMP算法—终于全部弄懂了

上篇书评-1：《最好的告别(Being Mortal)》

下篇机器学习-1：regression