吴恩达机器学习课笔记, 实例神经网络. 以AICS中为例
1 Neural Network
神经网络可以理解成抽象的神经元连接, 如果不引入非线性的函数, 其本质和线性回归差别不大.
神经网络中, 多层网络是在自动提取特征. 逐渐从小特征到大特征.
这里直接举出实例来表现: 手写阿拉伯数字的识别.
1.1 手写数字识别网络结构
搭建神经网络如下图:

1.1.1 全连接层(FullyConnectedLayer)
class FullyConnectedLayer(object):
def __init__(self, num_input, num_output): # 全连接层初始化
self.num_input = num_input
self.num_output = num_output
print('\tFully connected layer with input %d, output %d.' % (self.num_input, self.num_output))
def init_param(self, std=0.01): # 参数初始化
self.weight = np.random.normal(loc=0.0, scale=std, size=(self.num_input, self.num_output))
self.bias = np.zeros([1, self.num_output])
def forward(self, input): # 前向传播计算
start_time = time.time()
self.input = input
# TODO:全连接层的前向传播,计算输出结果
self.output = np.mat
return self.output
def backward(self, top_diff): # 反向传播的计算
self.d_weight = np.mat(self.input.T, top_diff)
self.d_bias = np.matmul(np.ones([1, top_diff.shape[0]]), top_diff)
bottom_diff = np.matmul(top_diff, self.weight.T)
return bottom_diff
def update_param(self, lr): # 参数更新
self.weight = self.weight - lr * self.d_weight
self.bias = self.bias - lr * self.d_bias
def load_param(self, weight, bias): # 参数加载
assert self.weight.shape == weight.shape
assert self.bias.shape == bias.shape
self.weight = weight
self.bias = bias
def save_param(self): # 参数保存
return self.weight, self.bias
全连接层以一维向量作为输入,输入与权重相乘后再与偏置相加得到输出向量. 是计算的主要层.
假设全连接层的输入为一维向量$\vec{x}$,维度为m;输出为一维向量y,维度为 n;权重 $W$ 是二维矩阵,维度为 m × n,偏置 b 是一维向量(也可以整个层用一个值替代),维度为 n。前向传播(forward)时,全连接层的输出的计算公式为
\[\vec{y} = W^T\vec{x} + b\]这里和线性回归一致.
在计算全连接层的反向传播时,给定神经网络损失函数 L 对当前全连接层的输出 y 的偏导$\nabla_yL = \frac{\partial L}{\partial y}$,其维度与全连接层的输出 y 相同,均为 n。
实际应用中通常使用批量随机梯度下降算法进行反向传播计算,即选择若干个样本同时计算。假设选择的样本量为 p,此时输入变为二维矩阵 X,维度为 p×m,每行代表一个样本。输出也变为二维矩阵 Y,维度为 p×n。
1.1.2 ReLU激活函数层
就是一个$\max(0,x)$的非线性函数.
1.1.3 Softmax损失层
计算损失函数, 并且归一化. 可以理解为多维的sigmoid函数.
1.2 模型构建
我们按照构建顺序来讲解各层和NN构建.
1.2.1 主函数
if __name__ == '__main__':
mlp = build_mnist_mlp()
evaluate(mlp)
这里分成两部, 一部分是构建模型, 另一部分是评估模型.
评估有很多种方法, 比较简单的就是将数据分为训练集(train set)和测试集(test/validation set). 训练后从测试集上评估结构, 防止过拟合等情况出现.
具体的优化方法由于笔者还远未入门, 所以等以后在学习.
接下来看构建模型.
1.2.2 构建模型
def build_mnist_mlp(param_dir='weight.npy'):
h1, h2, e = 32, 16, 10
mlp = MNIST_MLP(hidden1=h1, hidden2=h2, max_epoch=e)
mlp.load_data()
mlp.build_model()
mlp.init_model()
mlp.train()
mlp.save_model('mlp-%d-%d-%depoch.npy' % (h1, h2, e))
return mlp
其中h1和h2都是隐层神经元个数.
所谓隐层, 就是除开输出和输入两个层之间的所有层.
而e为训练代数, 此处就为训练10次.
第二行构建一个mlp类返回, 接下来这个mlp会读入数据, 构建模型等操作. 我们一步一步来.
首先是参数初始化:
class MNIST_MLP(object):
def __init__(self, batch_size=100, input_size=784, hidden1=32, hidden2=16, out_classes=10, lr=0.01, max_epoch=1, print_iter=100):
self.batch_size = batch_size
self.input_size = input_size
self.hidden1 = hidden1
self.hidden2 = hidden2
self.out_classes = out_classes
self.lr = lr
self.max_epoch = max_epoch
self.print_iter = print_iter
各个参数具体含义之后再讲.
接下来读入数据:
1.2.3 MNIST
def load_data(self):
print('Loading MNIST data from files...')
train_images = self.load_mnist(os.path.join(MNIST_DIR, TRAIN_DATA), True)
train_labels = self.load_mnist(os.path.join(MNIST_DIR, TRAIN_LABEL), False)
test_images = self.load_mnist(os.path.join(MNIST_DIR, TEST_DATA), True)
test_labels = self.load_mnist(os.path.join(MNIST_DIR, TEST_LABEL), False)
self.train_data = np.append(train_images, train_labels, axis=1)
self.test_data = np.append(test_images, test_labels, axis=1)
读入需要按照MNIST数据集结构来读入:
MNIST数据集(Mixed National Institute of Standards and Technology database)是美国国家标准与技术研究院收集整理的大型手写数字数据库,包含60,000个示例的训练集以及10,000个示例的测试集.
其格式如下:
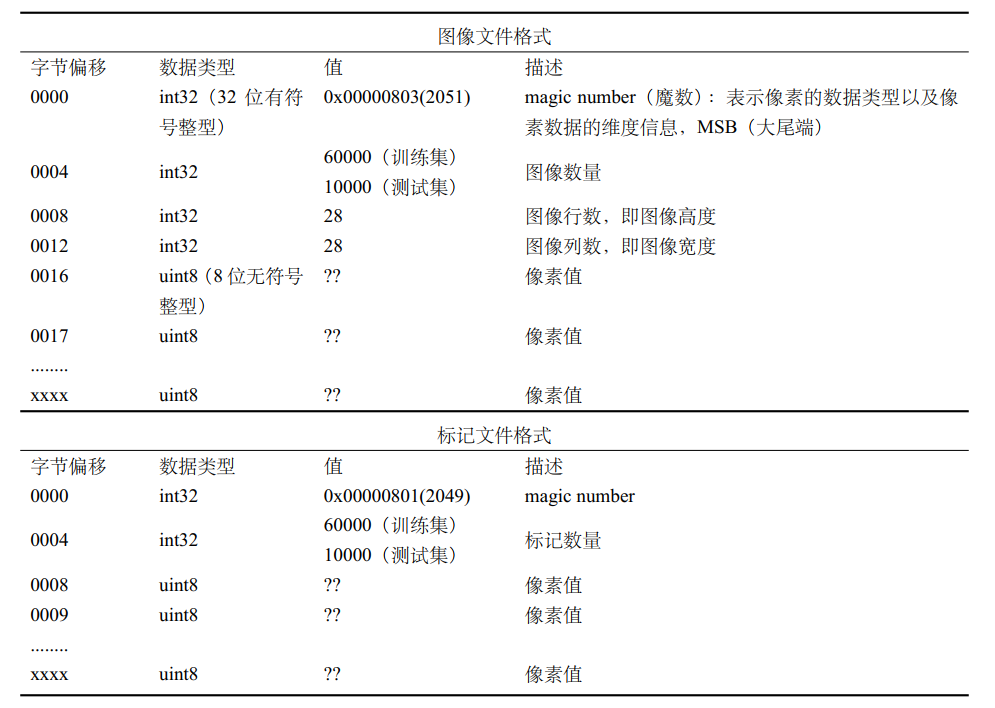
所以有读入函数:
def load_mnist(self, file_dir, is_images = 'True'):
# Read binary data
bin_file = open(file_dir, 'rb')
bin_data = bin_file.read()
bin_file.close()
# Analysis file header
if is_images:
# Read images
fmt_header = '>iiii'
magic, num_images, num_rows, num_cols = struct.unpack_from(fmt_header, bin_data, 0)
else:
# Read labels
fmt_header = '>ii'
magic, num_images = struct.unpack_from(fmt_header, bin_data, 0)
num_rows, num_cols = 1, 1
data_size = num_images * num_rows * num_cols
mat_data = struct.unpack_from('>' + str(data_size) + 'B', bin_data, struct.calcsize(fmt_header))
mat_data = np.reshape(mat_data, [num_images, num_rows * num_cols])
print('Load images from %s, number: %d, data shape: %s' % (file_dir, num_images, str(mat_data.shape)))
return mat_data
简单说一下
fmt_header,>表示大尾端,iiii表示读出四个有符号整数; 后面的B代表无符号字节(或者unsigned char); 更多请看FormatString
如果是图像信息, 则读出魔数, 图像个数, 单幅图像的行列共四个信息.
如果是标记信息, 则只需要读出魔数和图像个数, 接下来每个字节都是对应图像的数字值.
最后返回一个num_image行, 每行长num_rows * num_cols的二维矩阵.
回到load_data()中, 最后使用np.append(... axis = 1)将标记数据添加到行末位. 也就是数据变成: num_image行, 每行初始为num_rows*num_cols的图像, 和最后一个0-9的数字表示结果
并将这些存储到mlp中.
自此, 建立的模型的第一步, 读入数据完成. 接下来看搭建网络.
1.2.4 搭建网络
def build_model(self): # 建立网络结构
print('Building multi-layer perception model...')
self.fc1 = FullyConnectedLayer(self.input_size, self.hidden1)
self.relu1 = ReLULayer()
self.fc2 = FullyConnectedLayer(self.hidden1, self.hidden2)
self.relu2 = ReLULayer()
self.fc3 = FullyConnectedLayer(self.hidden2, self.out_classes)
self.softmax = SoftmaxLossLayer()
self.update_layer_list = [self.fc1, self.fc2, self.fc3]
设置各层如初始图一致.
随后初始化:
def init_model(self):
print('Initializing parameters of each layer in MLP...')
for layer in self.update_layer_list:
layer.init_param()
1.2.5 训练网络
def train(self):
max_batch = self.train_data.shape[0] / self.batch_size
print('Start training...')
for idx_epoch in range(self.max_epoch):
self.shuffle_data()
for idx_batch in range(max_batch):
batch_images = self.train_data[idx_batch*self.batch_size:(idx_batch+1)*self.batch_size, :-1]
batch_labels = self.train_data[idx_batch*self.batch_size:(idx_batch+1)*self.batch_size, -1]
prob = self.forward(batch_images)
loss = self.softmax.get_loss(batch_labels)
self.backward()
self.update(self.lr)
if idx_batch % self.print_iter == 0:
print('Epoch %d, iter %d, loss: %.6f' % (idx_epoch, idx_batch, loss))
确定训练批次, 为图像总数/每次大小. 每次一次完成的训练即为一次epoch.
随后利用np.random.shuffle打乱数据顺序, 防止固定的训练顺序导致结果类似.
对每一次周期内的分批次训练. 由之前的数据分析可知, :-1是取到label之前, 而-1则是取最后的label, 随后开始前向传播-损失计算-后向传播.
1.2.6 保存参数
mlp.save_model('mlp-%d-%d-%depoch.npy' % (h1, h2, e))
最后保存下参数, 防止每次都要训练.
接下来我们深入1.2.5中的训练过程.
1.3 训练过程
着重分析这一段:
prob = self.forward(batch_images)
loss = self.softmax.get_loss(batch_labels)
self.backward()
self.update(self.lr)
1.3.1 forward
前向传播如下:
def forward(self, input): # 神经网络的前向传播
h1 = self.fc1.forward(input)
h1 = self.relu1.forward(h1)
h2 = self.fc2.forward(h1)
h2 = self.relu2.forward(h2)
h3 = self.fc3.forward(h2)
prob = self.softmax.forward(h3)
return prob
先看全连接层的forward:
def forward(self, input): # 前向传播计算
self.input = input
# y = X * W + b
#self.output = np.matmul(self.input, self.weight) + self.bias
self.output = self.input.dot(self.weight) + self.bias
return self.output
直接相乘即可
relu则是 output = np.maximum(0, self.input)输出即可;
softmax则有些不同:
def forward(self, input): # 前向传播的计算
input_max = np.max(input, axis=1, keepdims=True)
input_exp = np.exp(input - input_max)
""" prob = exp(input-input_max) / sum(exp(input-input_max))"""
self.prob = input_exp / np.sum(input_exp, axis=1, keepdims=True)
return self.prob
以上就是直接的公式实现即可.
1.3.2 loss
损失层是为了衡量当前结果和最终目标之间的差距, 可以说是训练的监督员:
def get_loss(self, label): # 计算损失
self.batch_size = self.prob.shape[0]
self.label_onehot = np.zeros_like(self.prob)
self.label_onehot[np.arange(self.batch_size), label] = 1.0
loss = -np.sum(np.log(self.prob) * self.label_onehot) / self.batch_size
return loss
softmax层利用交叉熵来计算损失. 实现如上.
1.3.3 backward
后向传播是神经网络的调整过程, 大致如下:
def backward(self): # 神经网络的反向传播
dloss = self.softmax.backward()
dh3 = self.fc3.backward(dloss)
dh2 = self.relu2.backward(dh3)
dh2 = self.fc2.backward(dh2)
dh1 = self.relu1.backward(dh2)
dh1 = self.fc1.backward(dh1)
首先是softmax计算出损失, 然后逐层后向传递.
def backward(self): # 反向传播的计算
""" diff = 1/p * (y_h - y) """
bottom_diff = (self.prob - self.label_onehot) / self.batch_size
return bottom_diff
全连接层后向传播:
def backward(self, top_diff): # 反向传播的计算
self.d_weight = np.matmul(self.input.T, top_diff)
self.d_bias = np.matmul(np.ones([1, top_diff.shape[0]]), top_diff)
bottom_diff = np.matmul(top_diff, self.weight.T)
return bottom_diff
ReLU层后向传播:
def backward(self, top_diff): # 反向传播的计算
bottom_diff = top_diff * (self.input >= 0.)
return bottom_diff
如此反复就可以调整出最佳的参数模式.
之后会更新一个更复杂一点的VGG19的神经网络.